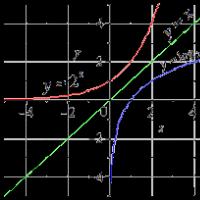
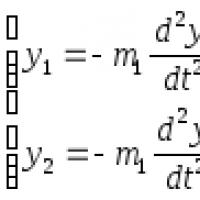Berilgan y 2x ning teskari funksiyasi. Funksiyalarning turlari. Teskari funksiya. Funksiyaning aniqlanish sohasi va qiymat sohasi. Teskari funktsiyani topish

Biz allaqachon shunday muammoga duch keldikki, berilgan f funktsiya va uning argumentining berilgan qiymati berilganda, bu nuqtada funktsiyaning qiymatini hisoblash kerak edi. Ammo ba'zida siz teskari muammoga duch kelishingiz kerak: ma'lum f funktsiya va uning ma'lum qiymati y berilgan, funktsiya berilgan y qiymatini oladigan argumentning qiymatini topish.

Har bir qiymatni o'z ta'rif sohasining bitta nuqtasida oladigan funksiya teskari funktsiya deb ataladi. Masalan, chiziqli funktsiya bo'ladi teskari funksiya. Ammo kvadratik funktsiya yoki sinus funksiya teskari funktsiyalar bo'lmaydi. Chunki funktsiya turli argumentlar bilan bir xil qiymatni qabul qilishi mumkin.

Teskari funksiya

Faraz qilaylik, f qandaydir ixtiyoriy teskari funksiyadir. y0 qiymatlari sohasidagi har bir raqam x0 ta'rif sohasidan faqat bitta raqamga to'g'ri keladi, f(x0) = y0.

Agar endi har bir x0 qiymatini y0 qiymati bilan bog'lasak, yangi funktsiyani olamiz. Masalan, f(x) = k * x + b chiziqli funksiya uchun g(x) = (x - b)/k funksiya unga teskari bo ladi.

Agar biron bir funktsiya bo'lsa g har bir nuqtada X f teskari funktsiya qiymatlari diapazoni f (y) = x qiymatni oladi, keyin biz funktsiyani aytamiz. g- f ga teskari funksiya mavjud.

Agar bizga qandaydir teskari f funktsiyaning grafigi berilsa, u holda teskari funktsiyaning grafigini qurish uchun quyidagi bayonotdan foydalanish mumkin: f funktsiyaning grafigi va g teskari funksiyasi to'g'ri chiziqqa nisbatan simmetrik bo'ladi. y = x tenglama bilan belgilangan chiziq.

Agar g funktsiya f funktsiyaga teskari funktsiya bo'lsa, u holda g funktsiya teskari funktsiya bo'ladi. f funksiya esa g funktsiyaga teskari funktsiya bo'ladi. Odatda ikkita f va g funksiyalar bir-biriga teskari, deyiladi.

Quyidagi rasmda f va g funksiyalarning bir-biriga o'zaro teskari grafiklari ko'rsatilgan.

Quyidagi teoremani keltiraylik: agar f funktsiya A oraliqda ortib ketsa (yoki kamaysa), u teskari bo'ladi. f funktsiyasi qiymatlari oralig'ida aniqlangan teskari funktsiya g, shuningdek, ortib borayotgan (yoki mos ravishda kamayuvchi) funktsiyadir. Bu teorema deyiladi teskari funksiya teoremasi.

Faraz qilaylik, ma'lum y = f (x) funksiyaga egamiz, u qat'iy monotonik (kamayuvchi yoki ortib boruvchi) va x ∈ a ta'rif sohasi bo'yicha uzluksiz; b ; uning qiymatlari diapazoni y ∈ c ; d, va c oralig'ida; d bu holda biz a qiymatlari diapazoniga ega x = g (y) aniqlangan funktsiyaga ega bo'lamiz; b. Ikkinchi funktsiya ham uzluksiz va qat'iy monotonik bo'ladi. y = f (x) ga nisbatan u teskari funktsiya bo'ladi. Ya'ni, y = f (x) berilgan oraliqda yoki kamayishi yoki ortishi bilan x = g (y) teskari funksiya haqida gapirish mumkin.

Bu ikki funktsiya, f va g, o'zaro teskari bo'ladi.

Nega bizga teskari funksiyalar tushunchasi kerak?

Bu bizga ushbu ifodalar yordamida aniq yozilgan y = f (x) tenglamalarini yechish uchun kerak.

Aytaylik, cos (x) = 1 3 tenglamaning yechimini topishimiz kerak. Uning yechimlari barcha nuqtalar bo'ladi: x = ± a rc c o s 1 3 + 2 p · k, k ∈ Z.

Masalan, teskari kosinus va kosinus funktsiyalari bir-biriga teskari bo'ladi.

Berilganlarga teskari bo‘lgan funksiyalarni topish uchun bir qancha masalalarni ko‘rib chiqamiz.

1-misol

Vaziyat: y = 3 x + 2 uchun teskari funksiya nima?

Yechim

Shartda ko'rsatilgan funksiyaning ta'riflar sohasi va qiymatlari diapazoni barcha haqiqiy sonlar to'plamidir. Bu tenglamani x orqali, ya’ni x ni y orqali ifodalash orqali yechishga harakat qilaylik.

Biz x = 1 3 y - 2 3 ni olamiz. Bu bizga kerak bo'lgan teskari funktsiya, lekin bu erda y argument, x esa funksiya bo'ladi. Keling, ko'proq tanish belgilar olish uchun ularni qayta tartibga solamiz:

Javob: y = 1 3 x - 2 3 funktsiyasi y = 3 x + 2 ga teskari bo'ladi.

Ikkala o'zaro teskari funktsiyani quyidagicha tasvirlash mumkin:

Ikkala grafikning y = x ga nisbatan simmetriyasini ko'ramiz. Bu chiziq birinchi va uchinchi kvadrantlarning bissektrisasidir. Biz o'zaro teskari funktsiyalarning xususiyatlaridan birining isbotini oldik, biz buni keyinroq muhokama qilamiz.

Keling, berilgan ko'rsatkichli funktsiyaga teskari bo'lgan logarifmik funktsiyani topishimiz kerak bo'lgan misolni olaylik.

2-misol

Vaziyat: y = 2 x uchun qaysi funktsiya teskari bo'lishini aniqlang.

Yechim

Berilgan funksiya uchun aniqlanish sohasi barcha haqiqiy sonlardir. Qiymatlar oralig'i 0 oralig'ida joylashgan; + ∞ . Endi biz x ni y hisobida ifodalashimiz, ya'ni belgilangan tenglamani x hisobida yechishimiz kerak. Biz x = log 2 y ni olamiz. O'zgaruvchilarni qayta joylashtiramiz va y = log 2 x ni olamiz.

Natijada, biz eksponensial va logarifmik funktsiyalarni oldik, ular butun ta'rif sohasi bo'ylab bir-biriga teskari bo'ladi.

Javob: y = log 2 x.

Grafikda ikkala funktsiya quyidagicha ko'rinadi:

O'zaro teskari funksiyalarning asosiy xossalari

Ushbu paragrafda o'zaro teskari bo'lgan y = f (x) va x = g (y) funktsiyalarining asosiy xususiyatlarini sanab o'tamiz.

Ta'rif 1

1. Biz allaqachon birinchi xususiyatni oldik: y = f (g (y)) va x = g (f (x)).
2. Ikkinchi xususiyat birinchisidan kelib chiqadi: y = f (x) ta'rif sohasi x = g (y) teskari funktsiyaning qiymatlari oralig'iga to'g'ri keladi va aksincha.
3. Teskari bo'lgan funksiyalarning grafiklari y = x ga nisbatan simmetrik bo'ladi.
4. Agar y = f (x) ortib borayotgan bo'lsa, u holda x = g (y) ortadi va y = f (x) kamayib borayotgan bo'lsa, x = g (y) ham kamayadi.

Biz sizga funksiyalarning ta'rif sohasi va ma'no sohasi tushunchalariga jiddiy e'tibor qaratishingizni va ularni hech qachon chalkashtirmaslikni maslahat beramiz. Faraz qilaylik, y = f (x) = a x va x = g (y) = log a y ikkita o'zaro teskari funktsiyaga egamiz. Birinchi xususiyatga ko'ra, y = f (g (y)) = a log a y. Bu tenglik faqat y ning musbat qiymatlari uchun to'g'ri bo'ladi va manfiy qiymatlar uchun logarifm aniqlanmagan, shuning uchun log a y = y ekanligini yozishga shoshilmang. Bu faqat y ijobiy bo'lganda to'g'ri ekanligini tekshiring va qo'shing.

Ammo x = f (g (x)) = log a a x = x tengligi x ning har qanday haqiqiy qiymatlari uchun to'g'ri bo'ladi.

Buni unutmang, ayniqsa trigonometrik va teskari trigonometrik funktsiyalar bilan ishlashingiz kerak bo'lsa. Demak, a r c sin sin 7 p 3 ≠ 7 p 3, chunki arksinus diapazoni p 2; p 2 va 7 p 3 unga kiritilmagan. To'g'ri kirish bo'ladi

a r c sin sin 7 p 3 = a r c sin sin 2 p + p 3 = = a r c sin sin p 3 = p 3

Lekin sin a r c sin 1 3 = 1 3 to'g'ri tenglik, ya'ni. sin (a r c sin x) = x uchun x ∈ - 1 ; 1 va x ∈ - p 2 uchun a r c sin (sin x) = x; p 2. Har doim teskari funktsiyalar oralig'i va ko'lami bilan ehtiyot bo'ling!

• Asosiy o'zaro teskari funktsiyalar: quvvat funktsiyalari

Agar bizda y = x a quvvat funksiyasi bo'lsa, u holda x > 0 uchun x = y 1 a quvvat funktsiyasi ham unga teskari bo'ladi. Harflarni almashtiramiz va mos ravishda y = x a va x = y 1 a ni olamiz.

Grafikda ular shunday ko'rinadi (musbat va manfiy koeffitsient a bo'lgan holatlar):

• Asosiy o'zaro teskari funktsiyalar: ko'rsatkichli va logarifmik

Keling, a ni olaylik, bu 1 ga teng bo'lmagan musbat son bo'ladi.

a > 1 va a bo'lgan funksiyalar uchun grafiklar< 1 будут выглядеть так:

• Asosiy o'zaro teskari funktsiyalar: trigonometrik va teskari trigonometrik

Agar biz sinus va arksinusning asosiy novdasini chizmoqchi bo'lsak, u shunday ko'rinadi (ta'kidlangan yorug'lik maydoni sifatida ko'rsatilgan).

Dars maqsadlari:

Tarbiyaviy:

• dastur materialiga muvofiq yangi mavzu bo'yicha bilimlarni rivojlantirish;
• funksiyaning qaytuvchanlik xossasini o‘rganish va berilgan funksiyaning teskari funksiyasini topishni o‘rgatish;

Rivojlanish:

• o'z-o'zini nazorat qilish ko'nikmalarini, mazmunli nutqni rivojlantirish;
• teskari funksiya tushunchasini o‘zlashtirish va teskari funksiyani topish usullarini o‘rganish;

Tarbiyaviy: kommunikativ kompetentsiyani rivojlantirish.

Uskunalar: kompyuter, proyektor, ekran, interfaol doska SMART doska, guruhlarda ishlash uchun tarqatma materiallar (mustaqil ish).

Darslar davomida.

1. Tashkiliy moment.

Maqsad – talabalarni sinfda ishlashga tayyorlash:

Ishda qatnashmaganlar ta'rifi,

O`quvchilarning mehnatga kayfiyatini uyg`otish, e`tiborni tashkil etish;

Darsning mavzusi va maqsadini ayting.

2. Talabalarning asosiy bilimlarini yangilash. Frontal so'rov.

Maqsad - o'rganilayotgan nazariy materialning to'g'riligi va xabardorligini o'rnatish, o'tilgan materialni takrorlash.<Приложение 1 >

Talabalar uchun interfaol doskada funksiya grafigi ko‘rsatilgan. O'qituvchi vazifani tuzadi - funktsiya grafigini ko'rib chiqing va funksiyaning o'rganilgan xususiyatlarini sanab o'ting. Talabalar tadqiqot loyihasiga muvofiq funktsiyaning xususiyatlarini sanab o'tadilar. Funksiya grafigining o‘ng tomonida o‘qituvchi interfaol doskaga marker yordamida nom berilgan xossalarni yozadi.

Funktsiya xususiyatlari:

O'qish oxirida o'qituvchi bugun darsda funktsiyaning yana bir xususiyati - qaytaruvchanlik bilan tanishishlarini aytadi. Yangi materialni mazmunli o'rganish uchun o'qituvchi bolalarni dars oxirida o'quvchilar javob berishi kerak bo'lgan asosiy savollar bilan tanishishga taklif qiladi. Savollar oddiy doskaga yoziladi va har bir talaba tarqatma material sifatida (dars oldidan tarqatiladi)

1. Qaysi funksiya invertible deyiladi?
2. Har qanday funktsiya teskari bo'ladimi?
3. Qaysi funktsiya ma'lumotlarning teskarisi deyiladi?
4. Ta'rif sohasi va funktsiya qiymatlari to'plami va unga teskari qanday bog'liq?
5. Agar funktsiya analitik tarzda berilgan bo'lsa, teskari funktsiyani formula bilan qanday aniqlash mumkin?
6. Agar funktsiya grafik tarzda berilgan bo'lsa, uning teskari funktsiyasining grafigi qanday tuziladi?

3. Yangi materialni tushuntirish.

Maqsad - dastur materialiga muvofiq yangi mavzu yuzasidan bilim hosil qilish; funksiyaning qaytuvchanlik xossasini o‘rganish va berilgan funksiyaning teskari funksiyasini topishni o‘rgatish; mazmunli nutqni rivojlantirish.

O'qituvchi materialni paragrafdagi materialga mos ravishda taqdim etadi. Interfaol doskada oʻqituvchi taʼrif sohalari va qiymatlar toʻplami bir xil boʻlgan, lekin funksiyalaridan biri monotonik, ikkinchisi esa monoton boʻlmagan ikkita funksiyaning grafiklarini solishtiradi va shu bilan oʻquvchilarni invertibil funksiya tushunchasi bilan tanishtiradi. .

Shundan so‘ng o‘qituvchi teskari funksiya ta’rifini tuzadi va interfaol doskadagi monoton funksiya grafigi yordamida inversiyalanuvchi funksiya teoremasining isbotini o‘tkazadi.

1-ta’rif: y=f(x), x X funksiya chaqiriladi qaytariladigan, agar u X to'plamining faqat bitta nuqtasida o'z qiymatlaridan birini qabul qilsa.

Teorema: Agar y=f(x) funksiya X to‘plamda monoton bo‘lsa, u teskari bo‘ladi.

Isbot:

1. Funktsiyaga ruxsat bering y=f(x) tomonidan ortadi X qo'yib yubor x 1 ≠x 2- to'plamning ikkita nuqtasi X.
2. Aniqroq bo'lsak, ruxsat bering x 1< x 2.
   Keyin bu haqiqatdan x 1< x 2 shunga amal qiladi f(x 1) < f(x 2).
3. Shunday qilib, argumentning turli qiymatlari funktsiyaning turli qiymatlariga mos keladi, ya'ni. funksiya teskari.

(Teoremani isbotlash davom etar ekan, o'qituvchi chizma bo'yicha barcha kerakli tushuntirishlarni belgilash uchun markerdan foydalanadi)

Teskari funktsiyaning ta'rifini shakllantirishdan oldin o'qituvchi o'quvchilarga taklif qilingan funksiyalarning qaysi biri invertibil ekanligini aniqlashni so'raydi? Interfaol doska funksiyalarning grafiklarini ko'rsatadi va bir nechta analitik aniqlangan funktsiyalarni yozadi:

B)

G) y = 2x + 5

D) y = -x 2 + 7

O'qituvchi teskari funktsiyaning ta'rifi bilan tanishtiradi.

2-ta’rif: teskari funksiyasi bo‘lsin y=f(x) to'plamda aniqlanadi X Va E(f)=Y. Keling, har biriga mos kelaylik y dan Y bu yagona ma'no X, qaysi vaqtda f(x)=y. Keyin biz belgilangan funktsiyani olamiz Y, A X- funksiya diapazoni

Bu funksiya belgilangan x=f -1 (y) va funksiyaga teskari deyiladi y=f(x).

Talabalardan ta'rif sohasi va teskari funktsiyalar qiymatlari to'plami o'rtasidagi bog'liqlik haqida xulosa chiqarish so'raladi.

Berilgan funktsiyaning teskarisini qanday topish masalasini ko'rib chiqish uchun o'qituvchi ikkita talabani jalb qildi. Bir kun avval bolalar o‘qituvchidan berilgan funksiyaning teskari funksiyasini topishning analitik va grafik usullarini mustaqil tahlil qilish topshirig‘ini oldilar. O‘qituvchi o‘quvchilarni darsga tayyorlashda maslahatchi vazifasini bajargan.

Birinchi talabaning xabari.

Eslatma: funktsiyaning monotonligi yetarli teskari funksiyaning mavjudligi sharti. Lekin u emas zaruriy shart.

Talaba funksiya monoton emas, balki teskari bo‘lganda, funksiya monoton bo‘lmasa va teskari bo‘lmaganda, monoton va teskari bo‘lganda turli vaziyatlarga misollar keltirdi.

Keyin talaba talabalarni analitik berilgan teskari funksiyani topish usuli bilan tanishtiradi.

Algoritmni topish

1. Funktsiya monotonik ekanligiga ishonch hosil qiling.
2. X o‘zgaruvchisini y shaklida ifodalang.
3. O'zgaruvchilar nomini o'zgartiring. x=f -1 (y) o'rniga y=f -1 (x) yozing.

Keyin berilgan birining teskari funksiyasini topish uchun ikkita misol yechadi.

1-misol: y=5x-3 funksiya uchun teskari funksiya mavjudligini ko‘rsating va uning analitik ifodasini toping.

Yechim. Chiziqli funktsiya y=5x-3 R da aniqlanadi, R da ortadi va uning qiymatlar diapazoni R ga teng. Bu teskari funktsiya R da mavjudligini bildiradi. Uning analitik ifodasini topish uchun y=5x- tenglamani yeching. x uchun 3; olamiz Bu talab qilinadigan teskari funksiya. R bo'yicha aniqlanadi va ortib boradi.

2-misol: y=x 2, x≤0 funksiya uchun teskari funksiya mavjudligini ko‘rsating va uning analitik ifodasini toping.

Funktsiya uzluksiz, ta'rif sohasi bo'yicha monotonik, shuning uchun u teskari bo'ladi. Funktsiyaning ta'rif sohalari va qiymatlari to'plamini tahlil qilib, teskari funktsiyaning analitik ifodasi haqida tegishli xulosa chiqariladi.

Ikkinchi talaba bu haqda taqdimot qiladi grafik teskari funksiyani topish usuli. Tushuntirish jarayonida talaba interfaol doskaning imkoniyatlaridan foydalanadi.

y=f(x) funksiyaga teskari bo‘lgan y=f -1 (x) funksiyaning grafigini olish uchun y=f(x) funksiya grafigini to‘g‘ri chiziqqa nisbatan simmetrik o‘zgartirish kerak. y=x.

Interfaol doskada tushuntirish jarayonida quyidagi vazifa bajariladi:

Bir xil koordinatalar sistemasida funksiya grafigini va uning teskari funksiyasi grafigini tuzing. Teskari funksiya uchun analitik ifodani yozing.

4. Yangi materialni birlamchi mustahkamlash.

Maqsad - o'rganilayotgan materialni tushunishning to'g'riligi va xabardorligini o'rnatish, materialni birlamchi tushunishdagi kamchiliklarni aniqlash va ularni tuzatish.

Talabalar juftlarga bo'linadi. Ularga topshiriqlar varaqlari beriladi, ularda ular ishni juftlik bilan bajaradilar. Ishni bajarish vaqti cheklangan (5-7 daqiqa). Bir juft o'quvchi kompyuterda ishlaydi, bu vaqt ichida proyektor o'chadi va qolgan bolalar o'quvchilar kompyuterda qanday ishlayotganini ko'ra olmaydi.

Vaqt tugashi bilan (ko‘pchilik o‘quvchilar ishni bajargan deb taxmin qilinadi) interfaol doskada o‘quvchilarning ishi ko‘rsatiladi (proyektor qayta yoqiladi), u yerda topshiriq bajarilganligi tekshirish vaqtida aniqlanadi. juftlikda to‘g‘ri bajarildi. Agar kerak bo'lsa, o'qituvchi tuzatish va tushuntirish ishlarini olib boradi.

Juftlikda mustaqil ishlash<2-ilova >

5. Darsning xulosasi. Ma'ruzadan oldin berilgan savollarga to'g'ri keladi. Dars uchun baholarni e'lon qilish.

Uy vazifasi §10. № 10.6(a,c) 10.8-10.9(b) 10.12(b)

Algebra va tahlilning boshlanishi. 10-sinf Umumiy ta'lim muassasalari uchun 2 qismda (profil darajasi) / A.G.Denishcheva, T.A.; tomonidan tahrirlangan A.G. Mordkovich, M: Mnemosyne, 2007 yil

Teskari funktsiyaning ta'rifi va uning xossalari: to'g'ridan-to'g'ri va teskari funktsiyalarning o'zaro monotonligi haqida lemma; to'g'ridan-to'g'ri va teskari funksiyalar grafiklarining simmetriyasi; segment, interval va yarim oraliqda qat’iy monoton bo‘lgan funksiya uchun teskari funksiyaning mavjudligi va uzluksizligi haqidagi teoremalar. Teskari funksiyalarga misollar. Muammoni hal qilish misoli. Xususiyatlar va teoremalarning isbotlari.

Tarkib

Shuningdek qarang: Funksiyaning ta’rifi, yuqori va quyi chegaralari, monoton funksiyasi.

Ta'rif va xususiyatlar

Teskari funktsiyaning ta'rifi
Funktsiya X ta'rif sohasiga va Y qiymatlar to'plamiga ega bo'lsin. Va u mulkka ega bo'lsin:
Barcha uchun .
U holda Y to'plamning istalgan elementi uchun X to'plamning faqat bitta elementini bog'lash mumkin, buning uchun . Ushbu yozishmalar chaqirilgan funktsiyani belgilaydi teskari funktsiya ga.
.

Teskari funktsiya quyidagicha ifodalanadi:
;
Ta'rifdan kelib chiqadiki
Barcha uchun .

Barcha uchun ;
To`g`ri va teskari funksiyalar grafiklarining simmetriya xossasi

To'g'ri va teskari funksiyalarning grafiklari to'g'ri chiziqqa nisbatan simmetrikdir.
Intervaldagi teskari funksiyaning mavjudligi va uzluksizligi haqidagi teorema

Funktsiya uzluksiz va segmentda qat'iy ravishda ortib boruvchi (kamayuvchi) bo'lsin. Keyin teskari funktsiya aniqlangan va segmentda uzluksiz bo'lib, u qat'iy ravishda ortadi (kamayadi).

Ortib borayotgan funktsiya uchun. Kamaytirish uchun -.
Intervaldagi teskari funksiyaning mavjudligi va uzluksizligi haqidagi teorema

Funktsiya uzluksiz va ochiq chekli yoki cheksiz intervalda qat'iy ravishda ortib boruvchi (kamayuvchi) bo'lsin. Keyin teskari funktsiya aniqlangan va intervalda uzluksiz bo'lib, u qat'iy ravishda ortadi (kamayadi).
Ortib borayotgan funktsiya uchun.

Kamaytirish uchun: .

Xuddi shunday, biz yarim oraliqda teskari funksiyaning mavjudligi va uzluksizligi haqidagi teoremani shakllantirishimiz mumkin.

Agar funktsiya uzluksiz bo'lsa va yarim oraliqda qat'iy ortib borsa (kamaysa), u holda yarim oraliqda yoki teskari funktsiya aniqlanadi, bu qat'iy ortadi (kamayadi). Bu yerga .
Agar qat'iy ortib borayotgan bo'lsa, u holda intervallar va intervallarga mos keladi va . Agar qat'iy kamayib ketsa, u holda intervallar va intervallarga mos keladi va .

Teskari funksiyalarga misollar

arksinus

Grafiklar y = gunoh x va teskari funksiya y = arcsin x.

Trigonometrik funktsiyani ko'rib chiqing sinus: . U argumentning barcha qiymatlari uchun aniqlangan va uzluksiz, ammo monotonik emas. Biroq, ta'rif doirasini toraytirsangiz, monoton joylarni aniqlashingiz mumkin. Shunday qilib, segmentda funktsiya aniqlangan, uzluksiz, qat'iy ravishda ortib boradi va qiymatlarni oladi -1 oldin +1 . Shuning uchun u arksinus deb ataladigan teskari funktsiyaga ega. Arcsine domen va qiymatlar to'plamiga ega.

Logarifm

Grafiklar y = 2 x va teskari funksiya y = log 2 x.

Eksponensial funktsiya aniqlangan, uzluksiz va argumentning barcha qiymatlari uchun qat'iy ravishda ortib boradi. Uning qiymatlari to'plami ochiq intervaldir. Teskari funktsiya ikkita asosning logarifmidir. U domen va ma'nolar to'plamiga ega.

Kvadrat ildiz

Grafiklar y = x 2 va teskari funktsiya.

Quvvat funktsiyasi hamma uchun belgilangan va uzluksizdir. Uning qiymatlari to'plami yarim oraliqdir. Ammo bu argumentning barcha qiymatlari uchun monotonik emas. Biroq, yarim oraliqda u uzluksiz va qat'iy monoton ravishda ortadi. Shuning uchun, agar biz to'plamni aniqlash sohasi sifatida olsak, u holda kvadrat ildiz deb ataladigan teskari funktsiya mavjud. Teskari funktsiya sohaga va qiymatlar to'plamiga ega.

Misol. n darajali ildizning mavjudligi va yagonaligini isbotlash

n natural son bo'lgan tenglama haqiqiy manfiy bo'lmagan son, haqiqiy sonlar to'plamida yagona yechimga ega ekanligini isbotlang. Bu yechim a ning n ildizi deyiladi. Ya'ni, har qanday manfiy bo'lmagan sonning n darajasining yagona ildiziga ega ekanligini ko'rsatishingiz kerak.

x o'zgaruvchining funksiyasini ko'rib chiqing:
(P1) .

Keling, uzluksiz ekanligini isbotlaylik.
Davomiylik ta'rifidan foydalanib, biz buni ko'rsatamiz
.
Biz Nyutonning binomial formulasini qo'llaymiz:
(P2)
.
Funksiya chegaralarining arifmetik xossalarini qo‘llaylik. dan beri, u holda faqat birinchi had nolga teng emas:
.
Davomiyligi isbotlangan.

Funktsiya (A1) ning qat'iy ravishda oshib borishini isbotlaylik.
Tengsizliklar bilan bog'langan ixtiyoriy sonlarni olaylik:
, , .
Biz buni ko'rsatishimiz kerak. Keling, o'zgaruvchilarni kiritamiz. Keyin.
.
Chunki (A2) dan . Yoki

Qattiq o'sish isbotlangan.
Funktsiyaning qiymatlari to'plamini topamiz.
nuqtada,.
Keling, chegarani topaylik.
.
Buning uchun Bernulli tengsizligini qo'llaymiz. Bizda:
O'shandan beri, keyin va.
Cheksiz katta funksiyalar uchun tengsizliklar xossasini qo‘llasak, buni topamiz.

Teskari funktsiya teoremasiga ko'ra, teskari funksiya aniqlangan va intervalda uzluksizdir. Ya'ni, har bir kishi uchun tenglamani qondiradigan yagona mavjud. Bizda bo'lganligi sababli, bu har qanday , tenglama x sonining n darajali ildizi deb ataladigan yagona yechimga ega ekanligini anglatadi:
.

Xususiyatlar va teoremalarning isbotlari

To'g'ridan-to'g'ri va teskari funktsiyalarning o'zaro monotonligi haqidagi lemmani isbotlash

Funktsiya X ta'rif sohasiga va Y qiymatlar to'plamiga ega bo'lsin. Uning teskari funktsiyaga ega ekanligini isbotlaylik. Bunga asoslanib, biz buni isbotlashimiz kerak
Barcha uchun .

Buning aksini faraz qilaylik. Raqamlar bo'lsin, shuning uchun . Shunday bo'lsin. Aks holda, belgini shunday qilib o'zgartiramiz. Keyin f ning qat'iy monotonligi tufayli tengsizliklardan birini qondirish kerak:
agar f qat'iy ravishda ortib borayotgan bo'lsa;
agar f qat'iy kamayib borayotgan bo'lsa.
Ya'ni . Qarama-qarshilik paydo bo'ldi. Shuning uchun u teskari funktsiyaga ega.

Funktsiya qat'iy ravishda ortib borsin. Teskari funksiya ham qat’iy ortib borishini isbotlaylik. Keling, quyidagi belgini kiritamiz:
. Ya'ni, agar , keyin ekanligini isbotlashimiz kerak.

Buning aksini faraz qilaylik. Bo'lsin, lekin.

Agar, keyin. Bu holat yo'qoladi.

Mayli.

Keyin, funksiyaning qat'iy ortishi tufayli , yoki . Qarama-qarshilik paydo bo'ldi. Shuning uchun faqat imkoniyat bo'lishi mumkin.

Lemma qat'iy ortib borayotgan funktsiya uchun isbotlangan. Bu lemma qat'iy kamayuvchi funktsiya uchun xuddi shunday tarzda isbotlanishi mumkin.

To'g'ridan-to'g'ri va teskari funksiyalar grafiklarining simmetriyasi haqidagi xossani isbotlash
(2.1) .
To'g'ridan-to'g'ri funktsiya grafigida ixtiyoriy nuqta bo'lsin:
.
To'g'ri chiziqqa nisbatan A nuqtaga simmetrik nuqta teskari funksiya grafigiga tegishli ekanligini ko'rsatamiz:
(2.2) .
Teskari funktsiyaning ta'rifidan kelib chiqadiki

Shunday qilib, biz (2.2) ko'rsatishimiz kerak. y = f teskari funksiyaning grafigi-1(x) y = f to'g'ridan-to'g'ri funktsiya grafigiga simmetrikdir(x)

y = x to'g'ri chiziqqa nisbatan.
, .

A va S nuqtalardan koordinata o'qiga perpendikulyarlarni tushiramiz. Keyin

A nuqta orqali chiziqqa perpendikulyar chiziq chizamiz. Chiziqlar C nuqtada kesishsin. To'g'ri chiziqda S nuqtani shunday quramiz. U holda S nuqta to'g'ri chiziqqa nisbatan A nuqtaga simmetrik bo'ladi.
.

Uchburchaklarni ko'rib chiqing va . Ularning uzunligi teng ikki tomoni bor: va , va ular orasidagi teng burchaklar: . Shuning uchun ular bir-biriga mos keladi. Keyin
.
Uchburchakni ko'rib chiqing. O'shandan beri
.
Xuddi shu narsa uchburchak uchun ham amal qiladi:
.

Keyin
;
.

Endi biz topamiz va:
(2.2)
Shunday qilib, (2.2) tenglama:
(2.1) .

qanoatlantiriladi, chunki , va (2.1) bajariladi:
funktsiya grafigining to'g'ri chiziqqa nisbatan simmetrik aks ettirilgan barcha nuqtalari teskari funksiya grafigiga tegishli.
Keyin biz joylarni o'zgartirishimiz mumkin. Natijada biz bunga erishamiz
funktsiya grafigining to'g'ri chiziqqa nisbatan simmetrik aks ettirilgan barcha nuqtalari funksiya grafigiga tegishli.
Bundan kelib chiqadiki, va funksiyalarning grafiklari to'g'ri chiziqqa nisbatan simmetrikdir.

Mulk isbotlangan.

Intervaldagi teskari funksiyaning mavjudligi va uzluksizligi haqidagi teoremani isbotlash

Funksiyaning aniqlanish sohasi - segmentni belgilaymiz.

1. Funktsiya qiymatlari to'plami segment ekanligini ko'rsatamiz:
,
Qayerda.

Darhaqiqat, funksiya segmentda uzluksiz bo'lganligi sababli, Veyershtrass teoremasiga ko'ra, u minimal va maksimalga etadi. Keyin, Bolzano-Koshi teoremasi bo'yicha, funktsiya segmentdan barcha qiymatlarni oladi. Ya'ni, har kim uchun bor , buning uchun . Minimal va maksimal bo'lganligi sababli, funktsiya faqat segmentdagi to'plamdan qiymatlarni oladi.

2. Funksiya qat’iy monoton bo‘lgani uchun, yuqoridagiga ko‘ra, teskari funksiya mavjud bo‘lib, u ham qat’iy monoton (ko‘paysa ortadi, kamaysa kamayadi). Teskari funktsiyaning sohasi to'plam, qiymatlar to'plami esa to'plamdir.

3. Endi teskari funksiya uzluksiz ekanligini isbotlaymiz.

3.1. Kesimning ixtiyoriy ichki nuqtasi bo'lsin: . Bu nuqtada teskari funksiya uzluksiz ekanligini isbotlaylik.

Nuqta unga mos kelsin. Teskari funktsiya qat'iy monotonik bo'lgani uchun, ya'ni segmentning ichki nuqtasi:
.
Davomiylik ta'rifiga ko'ra, har qanday narsa uchun shunday funktsiya mavjudligini isbotlashimiz kerak
(3.1) Barcha uchun .

E'tibor bering, biz uni xohlaganimizcha olishimiz mumkin. Haqiqatan ham, agar biz tengsizliklar (3.1) ning etarlicha kichik qiymatlari uchun qanoatlantiriladigan funktsiyani topgan bo'lsak, ga qo'ysak, ular avtomatik ravishda har qanday katta qiymatlar uchun qondiriladi.

Keling, uni shunchalik kichik qilib olaylikki, nuqtalar segmentga tegishli:
.
Keling, belgini kiritamiz va tartibga keltiramiz:



.

Birinchi tengsizlikni (3.1) o'zgartiramiz:
(3.1) Barcha uchun .
;
;
;
(3.2) .
Bu qat'iy monotonik bo'lgani uchun, shundan kelib chiqadi
(3.3.1) , agar u ko'paysa;
(3.3.2) , agar u kamaysa.
Teskari funktsiya ham qat'iy monoton bo'lgani uchun (3.3) tengsizliklar (3.2) tengsizliklarni bildiradi.

Har qanday e uchun > 0 d bor, shuning uchun |f -1 (y) - f -1 (y 0) |< ε hamma uchun |y - y 0 | < δ .

Tengsizliklar (3.3) ochiq intervalni belgilaydi, uning uchlari nuqtadan masofalar va masofalarda joylashgan. Ushbu masofalarning eng kichiki bo'lsin:
.
, ning qat'iy monotonligi tufayli. Shunung uchun . U holda oraliq tengsizliklar (3.3) bilan aniqlangan oraliqda yotadi. Va unga tegishli barcha qiymatlar uchun tengsizliklar (3.2) qondiriladi.

Shunday qilib, biz kichik uchun etarli ekanligini topdik , there is , so that
da .
Endi belgini o'zgartiramiz.
Kichkina yetarlicha, bunday narsa bor, shuning uchun
da .
Bu ichki nuqtalarda teskari funksiya uzluksiz ekanligini bildiradi.

3.2. Endi ta'rif sohasining uchlarini ko'rib chiqing. Bu erda barcha mantiqlar bir xil bo'lib qoladi. Siz faqat ushbu nuqtalarning bir tomonlama mahallalarini hisobga olishingiz kerak. Nuqta o'rniga yoki, nuqta o'rniga - yoki bo'ladi.

Demak, ortib borayotgan funksiya uchun , .
da .
Teskari funktsiya nuqtada uzluksiz bo'ladi, chunki har qanday etarlicha kichik uchun mavjud bo'ladi, shuning uchun
da .

Kamayuvchi funktsiya uchun, .
Teskari funktsiya nuqtada uzluksiz bo'ladi, chunki har qanday etarlicha kichik uchun mavjud bo'ladi, shuning uchun
da .
Teskari funktsiya nuqtada uzluksiz bo'ladi, chunki har qanday etarlicha kichik uchun mavjud bo'ladi, shuning uchun
da .

Teorema isbotlangan.

Intervaldagi teskari funksiyaning mavjudligi va uzluksizligi haqidagi teoremani isbotlash

Funksiyaning aniqlanish sohasini - ochiq intervalni belgilaymiz. Uning qiymatlari to'plami bo'lsin. Yuqoridagilarga ko'ra, ta'rif sohasiga, qiymatlar to'plamiga ega bo'lgan va qat'iy monotonik (agar u ko'paysa ortadi va kamaysa kamayadi) bo'lgan teskari funksiya mavjud. Buni isbotlash biz uchun qoladi
1) to'plam ochiq intervaldir va bu
2) teskari funksiya unda uzluksiz.
Bu yerga .

1. Funktsiya qiymatlari to'plami ochiq intervalli ekanligini ko'rsatamiz:
.

Elementlari taqqoslash operatsiyasiga ega bo'lgan har qanday bo'sh bo'lmagan to'plam singari, funktsiya qiymatlari to'plami ham pastki va yuqori chegaralarga ega:
.
Bu yerda va chekli sonlar yoki belgilar va bo'lishi mumkin.

1.1. va nuqtalari funksiya qiymatlari to'plamiga tegishli emasligini ko'rsatamiz. Ya'ni, qiymatlar to'plami segment bo'lishi mumkin emas.

Agar yoki bo'lsa cheksizlikka nuqta: yoki , u holda bunday nuqta to'plamning elementi emas. Shuning uchun u bir nechta qiymatlarga tegishli bo'lishi mumkin emas.

(yoki ) chekli son bo'lsin. Buning aksini faraz qilaylik. Nuqta (yoki ) funksiya qiymatlari to‘plamiga tegishli bo‘lsin. Ya'ni, qaysi (yoki) uchun shunday bor. Keling, ballarni olamiz va tengsizliklarni qondiramiz:
.
Funktsiya qat'iy monotonik bo'lgani uchun
, agar f oshsa;
, agar f kamaysa.
Ya'ni, biz funktsiya qiymati kichik (katta) bo'lgan nuqtani topdik. Ammo bu pastki (yuqori) chegaraning ta'rifiga zid keladi, unga ko'ra
Barcha uchun .
Shuning uchun nuqtalar funktsiya qiymatlari to'plamiga tegishli bo'lishi mumkin emas.

1.2. Endi biz qiymatlar to'plami intervallar va nuqtalar birligi emas, balki interval ekanligini ko'rsatamiz. Ya'ni, har qanday nuqta uchun bor , qaysi uchun .

Infimum va supremum ta'riflariga ko'ra, nuqtalarning har qanday qo'shnisi va to'plamning kamida bitta elementini o'z ichiga oladi. Intervalga tegishli ixtiyoriy son bo'lsin: . Keyin mahalla uchun mavjud, buning uchun
.
Mahalla uchun bor , buning uchun
.

O'shandan beri va, keyin. Keyin
(4.1.1) ko'paysa;
(4.1.2) kamaysa.
Tengsizliklarni (4.1) qarama-qarshilik bilan isbotlash oson. Ammo siz foydalanishingiz mumkin, unga ko'ra to'plamda teskari funktsiya mavjud bo'lib, u ko'paysa qat'iy ortadi va kamaysa qat'iy kamayadi. Shunda biz darhol tengsizliklarni olamiz (4.1).

Shunday qilib, bizda bir segment bor, bu erda agar ortadi;
kamaysa.
Segmentning oxirida funktsiya va qiymatlarini oladi. Chunki, Bolzano-Koshi teoremasiga ko'ra, buning uchun bir nuqta bor.

O'shandan beri biz bu bilan har qanday odam uchun borligini ko'rsatdik. Bu funktsiyaning qiymatlar to'plami ochiq intervalli ekanligini anglatadi.

2. Endi teskari funksiya oraliqning ixtiyoriy nuqtasida uzluksiz ekanligini ko rsatamiz: . Buning uchun segmentga murojaat qiling. Chunki, teskari funksiya segmentda, shu jumladan nuqtada uzluksizdir.

Teorema isbotlangan.

Adabiyotlar:
O.I. Besov. Matematik tahlil bo'yicha ma'ruzalar. 1-qism. Moskva, 2004 yil.
SM. Nikolskiy. Matematik tahlil kursi. 1-jild. Moskva, 1983 yil.

Shuningdek qarang:

$X$ va $Y$ toʻplamlari haqiqiy sonlar toʻplamiga kiritilsin. teskari funksiya tushunchasini kiritamiz.

Ta'rif 1

$X$ toʻplamini $Y$ toʻplamiga moslashtiruvchi $f:X\to Y$ funksiyasi, agar X$ dagi $x_1,x_2\ elementlar uchun $x_1\ne x_2$ boʻlishidan kelib chiqib, invertible deyiladi. bu $f(x_1 )\ne f(x_2)$.

Endi biz teskari funksiya tushunchasini kiritishimiz mumkin.

Ta'rif 2

$X$ toʻplamini $Y$ toʻplamiga solishtiruvchi $f:X\to Y$ funksiyasi teskari boʻlsin. Keyin $f^(-1)\left(y\right)=x$ sharti bilan aniqlangan $Y$ toʻplamini $X$ toʻplamiga solishtiruvchi $f^(-1):Y\to X$ funksiyasi boʻladi. $f( x)$ uchun teskari deb ataladi.

Keling, teoremani tuzamiz:

Teorema 1

$y=f(x)$ funksiya aniqlansin, monoton ravishda ortib boruvchi (kamayuvchi) va $X$ oraliqda uzluksiz. Keyin ushbu funktsiya qiymatlarining mos keladigan $Y$ oralig'ida u teskari funktsiyaga ega bo'lib, u ham monoton ravishda oshadi (kamayadi) va $Y$ oralig'ida uzluksizdir.

Endi to'g'ridan-to'g'ri o'zaro teskari funktsiyalar tushunchasini kiritamiz.

Ta'rif 3

2-ta'rif doirasida $f(x)$ va $f^(-1)\left(y\right)$ funktsiyalari o'zaro teskari funksiyalar deb ataladi.

O'zaro teskari funksiyalarning xossalari

$y=f(x)$ va $x=g(y)$ funksiyalari oʻzaro teskari boʻlsin.

$y=f(g\chap(y\o'ng))$ va $x=g(f(x))$

$y=f(x)$ funksiyani aniqlash sohasi $\ x=g(y)$ funksiyaning qiymat sohasiga teng. $x=g(y)$ funksiyani aniqlash sohasi esa $\ y=f(x)$ funksiyaning qiymat sohasiga teng.

$y=f(x)$ va $x=g(y)$ funksiyalarning grafiklari $y=x$ toʻgʻri chiziqqa nisbatan simmetrikdir.

Agar funksiyalardan biri ortib (kamaysa), ikkinchi funksiya ortadi (kamayadi).

Teskari funktsiyani topish

$y=f(x)$ tenglama $x$ oʻzgaruvchisiga nisbatan yechilgan.

Olingan ildizlardan $X$ intervaliga tegishlilari topiladi.

Topilgan $x$ $y$ raqamiga mos keladi.

1-misol

$X=[-1,0]$ oraliqda $y=x^2$ funksiyasi uchun teskari funksiyani toping.

Bu funktsiya $X$ oralig'ida kamayuvchi va uzluksiz bo'lgani uchun, keyin $Y=$ oralig'ida, bu oraliqda ham kamayuvchi va uzluksiz (1-teorema).

$x$ ni hisoblaymiz:

\ \

Kerakli $x$ ni tanlang:

Javob: teskari funksiya $y=-\sqrt(x)$.

Teskari funksiyalarni topish masalalari

Bu qismda biz ba'zi elementar funksiyalar uchun teskari funksiyalarni ko'rib chiqamiz. Yuqorida keltirilgan sxema bo'yicha muammolarni hal qilamiz.

2-misol

$y=x+4$ funksiya uchun teskari funksiyani toping

$y=x+4$ tenglamasidan $x$ ni topamiz:

3-misol

$y=x^3$ funksiyasi uchun teskari funksiyani toping

Yechim.

Funktsiya butun ta'rif sohasi bo'ylab ortib borayotgan va uzluksiz bo'lganligi sababli, 1-teoremaga ko'ra, u teskari uzluksiz va ortib boruvchi funktsiyaga ega.

$y=x^3$ tenglamasidan $x$ topamiz:

$x$ mos qiymatlarini topish

Qiymat bizning holatlarimizga mos keladi (chunki ta'rif sohasi barcha raqamlardir)

O'zgaruvchilarni qayta aniqlaymiz, biz teskari funksiya shaklga ega ekanligini tushunamiz

4-misol

$$ oraliqda $y=cosx$ funksiyasi uchun teskari funksiya toping

Yechim.

$X=\left$ to'plamidagi $y=cosx$ funksiyasini ko'rib chiqaylik. U $X$ toʻplamida uzluksiz va kamayuvchi boʻlib, $X=\left$ toʻplamini $Y=[-1,1]$ toʻplamga moslashtiradi, shuning uchun teskari uzluksiz monoton funksiya mavjudligi haqidagi teorema boʻyicha, $Y$ toʻplamida $y=cosx$ funksiyasi $Y=[-1,1]$ toʻplamida ham uzluksiz va ortib boruvchi teskari funksiya mavjud va $[-1,1]$ toʻplamini xaritalaydi. $\left$ to'plamiga.

$y=cosx$ tenglamasidan $x$ topamiz:

$x$ mos qiymatlarini topish

O'zgaruvchilarni qayta aniqlaymiz, biz teskari funksiya shaklga ega ekanligini tushunamiz

5-misol

$\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ oraliqda $y=tgx$ funksiyasi uchun teskari funksiya toping.

Yechim.

$X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ toʻplamidagi $y=tgx$ funksiyasini koʻrib chiqing. U $X$ toʻplamida uzluksiz va ortib boradi va $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ toʻplamini $Y toʻplamiga moslashtiradi. =R$ demak, teskari uzluksiz monoton funksiya mavjudligi haqidagi teoremaga ko‘ra, $Y$ to‘plamdagi $y=tgx$ funksiya teskari funktsiyaga ega bo‘lib, u ham $Y=R to‘plamda uzluksiz va ortib boruvchi funktsiyaga ega. $ va $R$ toʻplamini $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$ toʻplamiga moslashtiradi.

$y=tgx$ tenglamasidan $x$ ni topamiz:

$x$ mos qiymatlarini topish

O'zgaruvchilarni qayta aniqlaymiz, biz teskari funksiya shaklga ega ekanligini tushunamiz