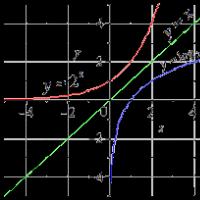
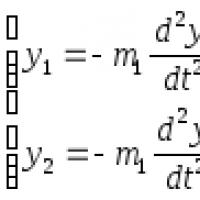Екі еркіндік дәрежесі бар жүйенің еркін тербелістері. Екі еркіндік дәрежесі бар жүйелердің еркін тербелістері Бас координаталарға көшу

Екі еркіндік дәрежесі бар жүйелер бірнеше еркіндік дәрежесі бар жүйелердің ерекше жағдайы болып табылады. Бірақ бұл жүйелер діріл жиіліктерін, амплитудаларын және динамикалық ауытқуларды анықтауға арналған есептеу формулаларын түпкілікті түрде алуға мүмкіндік беретін ең қарапайым болып табылады.

y Инерциялық күштердің әсерінен сәуленің ауытқуы:

P 2 =1 (1)

(1) өрнектеріндегі (-) белгілері инерциялық күштер мен бірліктерге байланысты. қозғалыстар қарама-қарсы бағытта болады.

Біз массалық тербелістер гармоникалық заң бойынша жүреді деп есептейміз:

(2)

Массалық қозғалыстың үдеуін табайық:

(3)

(2) және (3) өрнектерді (1) теңдеуге қойып, мынаны аламыз:

(5)

А 1 және А 2 белгісіз тербеліс амплитудаларын қарастырып, теңдеулерді түрлендіреміз:

(6)

А 1 = А 2 =0 біртекті теңдеулер жүйесінің шешімі бізге нөлдік емес шешімді алу үшін сәйкес келмейді, (6) жүйенің анықтауыштарын нөлге теңейміз;

(7)

Табиғи тербелістердің  белгісіз дөңгелек жиілігін ескере отырып (8) теңдеуді түрлендірейік:

(9) теңдеу екі еркіндік дәрежесі бар жүйелердің еркін тербелістерінің бигармониялық теңдеуі деп аталады.

 2 =Z айнымалысын ауыстырсақ, аламыз

осы жерден Z 1 және Z 2-ні анықтаймыз.

Нәтижесінде келесі қорытындылар жасауға болады:

1. Екі еркіндік дәрежесі бар жүйелердің еркін тербелісі екі  1 және  2 жиілікте болады. Төменгі жиілік 1 негізгі немесе негізгі тон, жоғары жиілік 2 екінші жиілік немесе овертон деп аталады.

n еркіндік дәрежесі бар жүйелердің еркін тербелістері n-еркін тербелістерден тұратын n-тондық.

2. m 1 және m 2 массалардың қозғалыстары келесі формулалармен өрнектеледі:

яғни тербелістер  1 жиілікте пайда болса, онда кез келген уақытта массалық қозғалыстар бірдей белгілерге ие болады.

Егер тербелістер тек  2 жиілікте болса, онда кез келген уақытта массалық қозғалыстар қарама-қарсы белгілерге ие болады.

 1 және  2 жиіліктегі массалардың бір мезгілде тербелістері кезінде жүйе негізінен  1 жиілікте тербеледі және бұл тербелістерге  2 жиіліктегі овертон сәйкес келеді.

Егер екі еркіндік дәрежесі бар жүйе  жиілігі бар қозғаушы күшке бағынатын болса, онда мыналар қажет:

  0,7  1 .

Дәріс 9

Шексіз еркіндік дәрежесі бар жүйелердің тербелісі.

Механикалық тербеліс теориясы технологияның барлық дерлік салаларында көптеген және өте алуан түрлі қолданбаларға ие. Әртүрлі механикалық жүйелердің мақсаты мен жобалық шешіміне қарамастан, олардың тербелісі бірдей физикалық заңдарға бағынады, оларды зерттеу серпімді жүйелердің тербелістері теориясының пәні болып табылады. Тербелістердің сызықтық теориясы барынша толық дамыған. Бірнеше еркіндік дәрежесі бар жүйелердің тербеліс теориясын 18 ғасырда Лагранж өзінің «Аналитикалық механика» атты классикалық еңбегінде берді.

Джозеф Луи Лагранж (1736 - 1813) - 19 жасынан Туриндегі математика профессоры. 1759 жылдан - Берлин Ғылым академиясының мүшесі, 1766 жылдан - президенті; 1787 жылдан бастап Парижде тұрды. 1776 жылы Петербург Ғылым академиясының құрметті шетелдік мүшесі болып сайланды.

19 ғасырдың аяғында Рэйли шексіз еркіндік дәрежесі бар жүйелердің тербелістерінің сызықтық теориясының негізін қалады (яғни, деформацияланатын жүйенің бүкіл көлеміне массаның үздіксіз таралуымен). 20 ғасырда сызықтық теория аяқталды деп айтуға болады (Бубнов-Галеркин әдісі, ол сонымен қатар дәйекті жуықтаулар арқылы жоғары тербеліс жиіліктерін анықтауға мүмкіндік береді).

Джон Уильям Стретт (Лорд Рэйли) (1842 - 1919) - ағылшын физигі, тербеліс теориясы бойынша бірқатар еңбектердің авторы.

Иван Григорьевич Бубнов (1872 - 1919) - кеме құрылысы механикасының негізін салушылардың бірі. Петербург политехникалық институтының профессоры, 1910 жылдан - Теңіз академиясында.

Борис Григорьевич Галеркин (1871-1945) - Ленинград политехникалық институтының профессоры.

Рэйлей формуласы серпімді жүйелердің діріл және тұрақтылық теориясында ең танымал. Рэйлей формуласын шығарудың негізінде жатқан идея келесіге келеді. Жиілігі  серпімді жүйенің моногармоникалық (бір тонды) еркін тербелістері кезінде оның нүктелерінің қозғалысы гармоникалық заңға сәйкес уақыт бойынша жүреді:

Мұндағы  1 (x,y,z),  2 (x,y,z),  3 (x,y,z) – қарастырылып отырған тербеліс формасын (амплитудасын) анықтайтын нүктенің кеңістіктік координаталарының функциялары.

Егер бұл функциялар белгілі болса, онда дененің кинетикалық және потенциалдық энергиясының қосындысы тұрақты болған жағдайдан еркін тербелістердің  жиілігін табуға болады. Бұл шарт тек бір белгісіз шаманы қамтитын теңдеуге әкеледі.

Алайда бұл функциялар алдын ала белгілі емес. Рэйлей әдісінің жетекші идеясы - бұл функцияларды таңдауды шекаралық шарттармен және тербелістердің күтілетін пішінімен сәйкестендіру.

Өзекшенің жазық иілу тербелістері үшін бұл идеяның орындалуын толығырақ қарастырайық, тербелістердің пішіні =(x) функциясымен сипатталады; Еркін тербелістер тәуелділікпен сипатталады

иілген сырықтың потенциалдық энергиясы

(2)

кинетикалық энергия

(3)

Қайда л- стерженнің ұзындығы, m=m(x) стерженнің бөлінген массасының интенсивтілігі;

Өзекшенің қисық осінің қисаюы - көлденең тербелістердің жылдамдығы;

Берілген (1)

.

(4)

(5)

Уақыт өте келе бұл шамалардың әрқайсысы үздіксіз өзгереді, бірақ энергияның сақталу заңына сәйкес олардың қосындысы тұрақты болып қалады, яғни.

немесе мұнда (4), (5) өрнектерді ауыстыру арқылы

(7)

Бұл Рэйлей формуласына әкеледі:

(8)

Егер массасы M i шоғырланған жүктер үлестірілген массасы m стерженьмен байланысты болса, онда Рэйлей формуласы келесідей болады:

(9)

Шығарудың бүкіл барысы, қабылданған болжамдар (шыбықтар майысуының техникалық теориясының негізділігі, серпімсіз кедергінің жоқтығы) шеңберінде бұл формуланың дәл екендігін көрсетеді, егер (x) тербелістердің шынайы түрі болса. . Алайда(x) функциясы алдын ала белгісіз. Рэйлей формуласының практикалық маңызы мынада: діріл пішінін(x) ескере отырып, оны табиғи жиілікті табуға болады. Бұл ретте шешімге жақындықтың азды-көпті маңызды элементі енгізіледі. Осы себепті Рэйлей формуласы кейде жуық формула деп аталады.

m=cosnt Тербеліс ретінде есептің кинематикалық шекаралық шарттарын қанағаттандыратын функцияны алайық:(x)=ax 2.

Біз анықтаймыз:

(8) формула бойынша

Бұл нәтиже нақты нәтижеден айтарлықтай ерекшеленеді

Граммель формуласы дәлірек, ол әлі Рэйлей формуласы сияқты танымал бола қоймаған (мүмкін оның салыстырмалы «жастығына» байланысты - ол 1939 жылы ұсынылған).

Өзекшенің еркін иілу тербелістері мәселесіне тағы да тоқталайық.

Өзекшенің еркін тербелістерінің көрсетілген түрі (x) болсын. Сонда максималды инерциялық күштердің интенсивтілігі m 2  өрнегімен анықталады, мұндағы, бұрынғыдай, m=m(x) – стерженнің бөлінген массасының интенсивтілігі  2 – табиғи жиіліктің квадраты; Бұл күштер ауытқулар максималды болған кезде көрсетілген мәнге жетеді, яғни. (x) функциясы арқылы анықталады.

Максималды инерциялық күштердің әсерінен болатын иілу моменттері бойынша ең жоғары потенциалдық иілу энергиясының өрнегін жазайық:

. (10)

Мұнда - m 2  жүктемеден болатын иілу моменттері. Шартты жүктеме m тудыратын иілу моментін белгілейік, яғни.  инерция күшінен 2 есе аз.

, (11)

және (10) өрнекті былай жазуға болады:

. (12)

Ең жоғары кинетикалық энергия, жоғарыдағыдай

. (13)

(12) және (13) өрнектерді теңестіре отырып, Граммель формуласына келеміз:

(14)

Бұл формуланы пайдаланып есептеу үшін алдымен қолайлы (x) функциясын көрсету керек. Осыдан кейін шартты жүктеме m=m(x)(x) анықталады және m шартты жүктемеден туындаған иілу өрнектері жазылады. (14) формуласы арқылы жүйенің табиғи тербеліс жиілігі анықталады.

Мысалы: (алдыңғыны қарастырайық)

ж

m(x)·(x)=max 2

ТЕОРИЯЛЫҚ МЕХАНИКА

ӘОЖ 531.8:621.8

Д.М.Кобылянский, В.Ф.Гоголин

ДЕНЕЛЕРДІҢ БІР ЕРКІНДІК ДӘРЕЖЕСІНДЕГІ АЙНАЛУЫ МЕН ДІРІЛІЛЕРІНІҢ СҮЙЕСІМДІЛІГІ

1а-суретте көрсетілгендей дененің барлық бағыттағы қозғалысына ғана кедергі болатын үш идеалды шектеу қойылған Т жазық денені қарастырайық. Қосылыстар тең бүйірлі үшбұрыштың төбелерінде орналасқан A, B, C нүктелері. Координаталар жүйесін оның центрі үшбұрыштың центрімен сәйкес келетін және оған теңестірілетіндей етіп таңдап алып (1а-сурет), байланыстардың координаталары: A(0;R), B(^l/3 /2) ; -R/2), C ^-Ld/e /2; -I/2), мұндағы I үшбұрыштың центрінен оның төбелеріне дейінгі қашықтық, яғни А, В, С нүктелері арқылы өтетін шеңбердің радиусы. Бұл қалыпта дененің бір еркіндік дәрежесі болады. А, В, С нүктелеріндегі оның шекарасының нормальдары жылдамдықтардың лездік центрі болатын бір нүктеде қиылысатын болса ғана. Әйтпесе, дененің еркіндік дәрежелерінің саны нөлге тең болады және ол тек трансляциялық қозғалып қана қоймай, айналмалы қозғалысты да орындай алмайды. Дене бір дәрежелі еркіндікке ие болғанда, ол жоғарыда аталған нормальдардың қиылысу нүктесіндегі лездік айналу орталығымен айнала бастайды. Бұл нүкте координаталар басы болсын, О нүктесі. Егер лездік айналу центрі өз орнын өзгертпесе, онда T денесінің жалғыз мүмкін пішіні центрі О нүктесінде болатын радиусы R шеңбері болады.

Мәселе туындайды: дененің қозғалатын орталыққа қатысты айналуына мүмкіндік беретін басқа пішіндер бар ма

дене денесі А,В,С үш нүктеден осы байланыстарды үзбей үздіксіз өтті ме? Бізге белгілі әдебиеттерде мұндай мәселе қарастырылмаған және, шамасы, бірінші рет шешіліп жатыр.

Бұл есепті шешу үшін алдымен АВС үшбұрышының қозғалысын Т денесімен байланысты Х1О1Y1 координаталар жүйесіне қатысты қатты дене ретінде қарастырамыз (1б-сурет). Сонда үшбұрыштың қозғалысы үшбұрыштың 360°-қа толық айналуы кезінде оның төбелері дененің шекарасында үздіксіз қалатындай болса, онда дене де қозғалмайтынға қатысты қажетті қозғалысты кері орындайтын болады. ABC үшбұрышы және онымен байланысты координаталар жүйесі XOU.

ABC үшбұрышының қозғалысын О центріне қатысты айналу және О центрінің ОіХі осі бойымен қозғалысын /(g), ОіУі осі бойымен g(t) арқылы анықтаймыз. Сонда А нүктесінің траекториясының параметрлік теңдеуі мынадай түрге ие болады: x = ryaSh +/(r); уі=г-єо,?ґ +g(t), ґє (1)

g=0 нүктесінде О O1 нүктесімен сәйкес келуі керек болғандықтан, /(0)= g(0)=0 шарты орындалуы керек. Біз r = 2n/3 бұрышы арқылы бұрылғанда А нүктесі В1 нүктесімен, В нүктесі С нүктесімен және С нүктесі сәйкес келуін талап етеміз.

А1 нүктесімен. r = 4n/3 бұрышы арқылы бұрылғанда А нүктесі С1 нүктесіне, В нүктесі А1 нүктесіне, С нүктесі В1 нүктесіне өтуі керек. Үшбұрыштың төбелерінің қозғалысына қойылатын осы талаптарды біріктіру айналу центрін жылжыту функцияларының мәндерінің шарттарына әкеледі /(0)=/(2 p/3)=/(4 p/3)= 0; g0)=g(2л/3)=g(4л/3)=0 . (2) (2) шарттар функциялардың кең класымен, атап айтқанда sin(3mt/2) түріндегі функциялармен қанағаттандырылады, мұнда m - бүтін сан және олардың келесі түрдегі жалпы айнымалы коэффициенттері бар сызықтық комбинациялары:

H (g) = ^ bt (g) 8Іп(3тґ / 2)

Сонымен қатар, ретінде

1-сурет. Есептеу схемасы: а) - қозғалмайтын дененің орны және оның ХОУ жүйесіндегі байланыстары; б) - X1O1U1 қозғалмайтын жүйенің денемен байланысқан орны, ал ABC үшбұрышымен байланысты жылжымалы XOU жүйесі.

Теориялық механика

2-сурет. Денелердің пішіндері және олардың айналу орталықтарының қозғалыс траекториялары

Күріш. 3. Бұрышпен бұрылу кезіндегі дененің жағдайы және оның айналу центрінің сәйкес қозғалыс траекториясы

(2) шартқа сәйкес параметрлері бар циклоидтар, трохоидтар, лемнискаттар сияқты тұйық қисықтарды анықтайтын функцияларды, орын ауыстыру функцияларын алуға болады. Бұл жағдайда барлық мүмкін болатын функциялар периодты 2n/3 периодты болуы керек.

Сонымен, /(^, g(t) (2) функцияларының мәндері бойынша шарттары бар параметрлік теңдеулер жүйесі (1) немесе олардың (3) түрінде T денесінің шекарасы үшін қажетті теңдеуді береді. 2-суретте тапсырманың шарттарын қанағаттандыратын мүмкін болатын дене пішіндерінің мысалдары көрсетілген. Әр фигураның ортасында айналу центрінің траекториясы O1 көрсетілген және бұл мысалдарды жақсырақ көрсету үшін A, B, C нүктелік байланыстары үлкейтілген Тұрақты коэффициенттері бар (3) өрнекпен анықталған класстың қарапайым түрлерінің де айналуын орындайтын денелердің шекараларын сипаттайтын қисықтардың жеткілікті кең жиынтығы бар екенін көрсетіңіз

тек бір еркіндік дәрежесімен бір мезгілде тербелістер. 2-суреттегі а), в) шекаралық қисықтар тек көлденең ось бойынша айналу центрінің қозғалысына сәйкес келеді.

ОіХі гармоникалық заңға сәйкес және көрініп тұрғандай, екі симметрия осіне ие және таза дөңес, сопақ болуы мүмкін (2а-сурет), немесе дөңестікті ойыспен біріктіруі мүмкін (2б-сурет). Айналу центрінің қозғалыс амплитудасы бірдей тік және көлденең гармоникалық заңмен шекаралық қисықтар симметриясын жоғалтады (2 c, г-сурет). Гармоникалық тербелістер жиілігінің дененің шекаралық қисық сызығының пішініне айтарлықтай әсері амплитудасы мен жиілігінің шекараның пішіні мен геометриялық қасиеттеріне әсерін толық талдаусыз 2 d, f-суретте көрсетілген. осы жұмыстағы қисықтар, 2-суретте келтірілген мысалдар қажетті пішінді таңдауда техникалық мәселелерді шешу мүмкіндігін көрсететінін атап өткім келеді.

дененің айналу қозғалысын айналу жазықтығындағы тербелістермен біріктіру.

Енді ABC үшбұрышымен байланысты XOU қозғалмайтын координаталар жүйесіне қатысты дененің қозғалысын, яғни X1O1U1 координаталар жүйесінен XOU координаталар жүйесіне жылжуын қарастыра отырып, дененің шекаралық қисық сызығының келесі параметрлік теңдеулерін аламыз. берілген бұрылу бұрышы p x = cosp-

Cosp(4)

немесе (1) теңдеулерін ескере отырып, (4) теңдеулер x = cosp- пішінін алады.

- [ R cos(t) + g (t) - g (p)] sin p, y = sin p +

Cos б.

(5) теңдеулер дененің кез келген нүктесінің траекториясын берілген полярлықтары бойынша сипаттауға мүмкіндік береді.

t-g.i m*4<. п-і

t-ÍLÍtWM. d-0

Күріш. 4. Денелердің айналуы мен дірілінің үйлесімділігін қамтамасыз ететін қосылыстардың әртүрлі саны бар дене пішіндерінің нұсқалары

нал координаттары R,t. Атап айтқанда, R=0, t=0 кезінде бізде Об координаталарының басымен, яғни айналу центрімен сәйкес келетін нүкте бар, оның траекториясы қарастырылып отырған схемада (5) теңдеулермен сипатталады. :

*0 = -f (ph) cos ph + g (ph) sin ph, y0 = - f (ph) sin ph- g (ph) cos r.

3-суретте φ бұрышы арқылы бұрылған кездегі дене позицияларының мысалы (2б-сурет) көрсетілген және әрбір фигураның ортасында айналу центрінің траекториясы көрсетілген.

Oi, осы бұрыш арқылы дененің айналуына сәйкес. Техникалық тұрғыдан анимация жасау қиын емес

Физикалық үлгінің орнына 3-суретте көрсетілген дене қозғалысы туралы, алайда журнал мақаласының шеңбері бұған тек электронды нұсқада рұқсат ете алады. Көрсетілген мысал әлі де болды

Қарастырылып отырған мәселенің жалпылауы дұрыс үшбұрыштың төбелерінде орналасқан, дененің тек ілгерілемелі қозғалыстарын болдырмайтын нүктелер түріндегі n идеалды байланыстар жүйесі болып табылады. Сондықтан, үшбұрыш жағдайындағы сияқты, дене айналу центріне қатысты айнала бастауы мүмкін, бұл нормальдардың дененің шекарасына қосылу нүктелеріндегі қиылысу нүктесі болып табылады. Бұл жағдайда OU осінде орналасқан және айналу центрінен H қашықтықта орналасқан А денесінің нүктесінің траекториясының теңдеуі (1) түрінде болады. Бұл жағдайда айналу центрін (2) жылжыту функцияларының мәндерінің шарттары қабылданады

Кобылянский Горбунов

Дмитрий Михайлович Валерий Федорович

Кафедраның аспиранты. стационарлық және - док. техника. ғылымдар, проф. бөлім жүз

көлік құралдары, стационарлық және көлік құралдары

f(2kp/p)=g(2kp/p)=0. (7)

(7) шарт периоды 2n/n болатын периодты функцияларға, мысалы 8м(n-m4/2), сондай-ақ олардың (3) түріндегі сызықтық комбинацияларына және тұйық қисықтарды сипаттайтын басқа функцияларға сәйкес келеді. Жоғарыда айтылғанға ұқсас дәлелдеу дененің пішінін, айналу кезіндегі орнын және айналу центрінің траекториясын айналумен сәйкес келетін тербелістермен есептеуге мүмкіндік беретін бірдей теңдеулерге (4-6) әкеледі. . Мұндай есептеулердің мысалы ретінде 4-суретті келтіруге болады, онда нүктелі сызық денелердің бастапқы орнын көрсетеді, тұтас сызық l/3 бұрыш арқылы айналу кезіндегі денелердің орнын көрсетеді, ал әрбір фигураның ортасында дененің толық айналуы кезінде айналу центрінің толық траекториясы. Бұл мысалда n-бұрыштың центрі ретінде O айналу центрінің көлденең қозғалысы ғана қарастырылғанымен, алынған нәтижелер айналу қозғалысын біріктіретін бір еркіндік дәрежесі бар дененің мүмкін болатын пішіндерінің кең ауқымын көрсетеді. төрт, бес және алты қосылыстардың қатысуымен тербелістермен.

Бір еркіндік дәрежесі бар денелердің айналу және тербеліс қозғалыстарының үйлесімділігін есептеудің нәтижесінде алынған әдісті үшінші координат бойынша қозғалыстарға және басқа координаталық жазықтықтардағы айналуларға тыйым салынған кеңістіктік денелер үшін де қосусыз қолдануға болады.

Гоголин Вячеслав Анатольевич

Dr. техника. ғылымдар, проф. бөлім қолданбалы математик және

Екі еркіндік дәрежесі бар жүйе жалпыланған координаталар болсын. Жүйенің кинетикалық және потенциалдық энергиясы (10.2) формулалармен берілген:

T және P функциялары сөзсіз оң, сондықтан:

(10.2) тармағын (10.12) орнына қойып, екі еркіндік дәрежесі бар жүйенің шағын тербелістері үшін дифференциалдық теңдеулерді аламыз:

Жүйенің тұрақты тепе-теңдік жағдайына сәйкес келетін нөлдік шешімі A=B=0. Нөлдік емес шешімдер үшін (10.15) қатынасты құрастырамыз:

Тұрақтылық теңсіздіктеріне байланысты (10.18-ге қатысты) квадраттық теңдеудің екі оң нақты түбірі бар. Оларды өсу ретімен орналастырайық:

Екінші негізгі діріл үшін:

(10.21)

Негізгі тербелістерге гармоникалық тербеліс жатады.

Кезекте және (10.16) ауыстырып, негізгі тербелістерде А және В амплитудалары арасындағы байланыстарды табамыз: . Факторлар меншікті коэффициенттер (амплитудалық таралу коэффициенттері) деп аталады. Олар оң және теріс болуы мүмкін. Негізгі тербелістегі екі координат бірдей фазада болғанда; at - антифазада.

Әрбір координат бойынша алынған қозғалыс екі негізгі тербелістің қосындысы болады:

(10.22)

мұндағы - бастапқы шарттарға байланысты, - бастапқы шарттарға тәуелді емес және тербелмелі жүйенің өзінің параметрлерімен анықталады. Жалпы жағдайда жиіліктер мен салыстыруға келмейтін, сондықтан алынған қозғалыс мерзімді болмайды.

1. Массалары m бірдей екі материалдық нүктеден және әрқайсысының ұзындығы екі өзекшеден құралған қос математикалық маятниктің табиғи жиіліктері мен тербелістерінің табиғи режимдерін (кіші) анықтаңыз.

Жалпы түрдегі ұқсас жүйе 2-мысалда (§34) қарастырылды. Онда алынған (2) және (3) формулаларды қолданайық.

Қашан, біз аламыз:

Тербелістер аз болғандықтан, екінші ретті кішіге дейін:

(3)

(1)-ден (3) ескере отырып:

(4)

(4) және (2) тармақтарын салыстыра отырып, мынаны байқаймыз:

(7.52) жиілік теңдеуін кеңейте отырып, мынаны аламыз:

(9.50)-ден таралу коэффициенттерін табамыз: .

Бірінші үлкен тербеліс:

Фаза бойынша қозғалыс - әр сәтте өзектер бір бағытта айналады.

Екінші негізгі күмән:

Антифазадағы қозғалыс - әр сәтте өзектер дәл қарама-қарсы бағытта айналады.

Діріл режимдері суретте көрсетілген. 50. Екінші негізгі дірілде қозғалыссыз қалатын ерекше F нүктесі бар. Мұндай нүктелер түйіндер деп аталады. О соңғы нүктесі түйін емес.

2. Массалары бар екі қатты дене және қаттылығы бар екі серіппелер тегіс горизонталь жазықтықта орналасқан және шағын сызықтық тербелістерді орындай алатын жүйеге біріктірілген.

Бірінші үлкен тербеліс:

Денелер фаза бойынша оңға немесе солға жылжиды. Екінші дененің тербеліс амплитудасы 1,62 есе артық.

Екінші негізгі күмән:

Денелер антифазада қозғалады: не бір-біріне, не түйінге қарай, не түйіннен алшақтайды. Екінші дененің тербеліс амплитудасы біріншісінің амплитудасының 0,62-ге тең.

Консервативті механикалық жүйенің тұрақты тепе-теңдік жағдайының айналасындағы қозғалыс теңдеулерінен

екі еркіндік дәрежесі жағдайында бізде:

(1)

(Сильвестр критерийі бойынша:

(1) тұрақты тепе-теңдік күйге жақын жерде екі еркіндік дәрежесі бар механикалық жүйенің шағын еркін тербелістерінің дифференциалдық теңдеулер жүйесі. Оның шешімі келесі түрде ізделеді:

(2)

Бұл шешімді кіші тербелістердің дифференциалдық теңдеулер жүйесіне ауыстыру мынаны береді:

(3)

А және В-ға қатысты бұл біртекті алгебралық теңдеулер жүйесі. Жүйенің анықтауышы нөлге тең болғанда оның тривиальды емес шешімі бар:

(4)

Бұл биквадрат теңдеу жиілік теңдеуі деп аталады, оның екі оң түбірі бар, олар кіші тербелістердің дифференциалдық теңдеулер жүйесінің екі шешіміне сәйкес келеді:

Осылайша, әрбір жалпыланған координата әртүрлі жиіліктегі екі тербелістің қосындысы ретінде табылады, олар деп аталады. негізгі ауытқулар . Бұл жағдайда (3) жүйеден келесідей негізгі тербелістердің амплитудалары бір-бірімен келесідей байланысады:

(5)

Қайда - форма факторлары негізгі ауытқулар.

Нәтижесінде еркін тербеліс (1) теңдеулерінің шешімі ақырында келесі форманы алады:

(6)

Кіріс жәшігі(6) амплитудалар және бастапқы фазалар,тербелістер бастапқы шарттардан анықталады.

Екі еркіндік дәрежесі бар механикалық жүйелердің еріксіз тербелістері. Динамикалық діріл сөндіргіш

Механикалық жүйелердегі қажетсіз тербелістерді жою деп аталады дірілден қорғау (демпферлік).Бұл жағдайда қолданылатын техникалық құрылғылар деп аталады діріл сөндіргіштер (демперлер).

Динамикалық демпфердің жұмыс істеу принципі бір координатаға сәйкес келетін мезгіл-мезгіл өзгеретін алаңдататын жалпылама күштің әрекеті басқа координатқа сәйкес келетін потенциалды жалпыланған күштің әрекетімен бейтараптанған кездегі антирезонанс құбылысын қолдануға негізделген.

Механикалық жүйеге консервативті күштерден басқа гармоникалық заң бойынша уақыт өте келе өзгеретін мазалаушы күш әсер етсін.

Бұл жағдайда механикалық жүйе қозғалысының дифференциалдық теңдеулері келесідей болады:

Сызықтық дифференциалдық біртекті емес (бұл жағдайда) теңдеулер жүйесінің жалпы шешімін екі шешімнің қосындысы ретінде іздейміз: , - біртекті дифференциалдық теңдеулер жүйесінің жалпы шешімі; -біртекті емес дифференциалдық теңдеулер жүйесін ішінара шешу.

Мазалаушы күштің уақытқа тәуелділігін ескере отырып, нысанда белгілі бір шешім ізделеді.

Оны дифференциалдық теңдеулер жүйесіне ауыстыру мынаны береді:

Бұл жүйені Крамер ережесі арқылы шешіп, аламыз

Өйткені ол жиілік теңдеуінің сол жағымен сәйкес келеді және жоғалады

мазалаушы күштің жиілігі табиғи жиіліктердің бірімен сәйкес келгенде

тербелістер немесе А және В коэффициенттері бұл жағдайда шексіздікке айналады. Осылайша, екі еркіндік дәрежесі бар жүйенің тербелістері бар екі резонанстық жиілік

Еріксіз дифференциалдық теңдеулер жүйесінің жалпы шешімі

дірілдер пішіні бар:

Көріп отырғанымыздай, тербелмелі жүйенің параметрлерін таңдау арқылы, мысалы, А = 0 шартының орындалуына қол жеткізуге болады, яғни бірінші жалпыланған координатаға сәйкес келетін мәжбүрлі тербелістердің амплитудасы нөлге айналады.

Бұл құбылыс антирезонанс деп аталады.

Қарастырылып отырған жағдайда бұл орын алады, егер

Әсер ету теориясының негізгі түсініктері мен гипотезалары. Әсер ету теориясының негізгі теңдеуі

Құбылыс, онда қысқа мерзімде, т. дерлік лезде материалдық объектілер нүктелерінің жылдамдықтары деп аталатын соңғы мәндерге өзгереді соққы .

Соққы кезінде жылдамдықтың соңғы өзгерісі өте қысқа уақыт аралығында болатындықтан, өте үлкен үдеулер, демек, өте үлкен күштер пайда болады. Бұл күштер өте қысқа уақыт аралығында әрекет етеді, бірақ олардың осы уақыт аралығындағы импульстері шекті шамалар.

Қысқа уақыт аралығындағы әсер ету кезінде пайда болатын, бірақ сонымен бірге үлкен мәнге жететін, олардың осы уақыт аралығындағы импульстері шекті мәндер болатын күштер деп аталады. соққы күштері .

Соққы созылатын қысқа уақыт кезеңі деп аталады әсер ету уақыты. Соққы кезіндегі соққы күштерінің импульстері деп аталады соққы импульстары .

Қарапайым (соққысыз) күштің әсерінен қозғалатын m массасы MT берілсін. Қарастырылған МТ жылдамдыққа ие болған сәтте – соғуға дейінгі жылдамдық, оған әсер ету күші әсер ете бастайды, оның әрекеті осы сәтте тоқтайды. Күштердің әсерінен және соққы уақытындағы МТ қозғалысын анықтайық.

Нүкте импульсінің өзгеруі туралы теореманы қолданып, мынаны аламыз:

,

соққыдан кейінгі сәттегі нүктенің жылдамдығы қайда.

Анықталған интегралдың орташа мәні туралы теореманы пайдаланып, мынаны жаза аламыз:

,

мұндағы және белгілі бір уақыт кезеңіндегі күштердің орташа мәндері. Оның үстіне бұл шекті шама; Соққы кезіндегі соққы күші өте үлкен мәнге жетеді (ретімен). Демек, өнім шектеулі мөлшер болып табылатын өніммен салыстырғанда шамалы болады.

Потенциалды өріс күштеріне және уақыт бойынша периодты түрде өзгеретін күштерге бағынатын екі еркіндік дәрежесі бар жүйенің шағын тербелістерін қарастырайық. Жүйенің нәтижесінде пайда болатын қозғалыстар мәжбүрлі тербелістер деп аталады.

Мазалайтын жалпыланған күштер уақыт бойынша гармоникалық заң бойынша өзгеріп, периодтары мен бастапқы фазалары бірдей болсын. Сонда қарастырылатын жүйенің қозғалыс теңдеулері келесідей болады:

Қарастырылып отырған жағдайдағы қозғалыс теңдеулері тұрақты коэффициенттері және оң жағы бар сызықтық екінші ретті дифференциалдық теңдеулер жүйесі болып табылады.

Негізгі координаттарға өтіңіз

Қозғалыс теңдеулерін зерттеуге ыңғайлы болу үшін жүйенің негізгі координаталарына көшейік, координаталар арасындағы байланыс форманың алдыңғы абзацының формулаларымен анықталады.

Қалыпты координаталарға сәйкес келетін жалпыланған күштерді сәйкесінше белгілейік, өйткені жалпыланған күштер жүйеге әсер ететін күштердің элементар жұмысын өрнектейтін жалпыланған координаттардың сәйкес вариациялары үшін коэффициенттерді білдіреді.

Демек:

Сонымен, негізгі координаталардағы қозғалыс теңдеулері келесі формада болады:

Қалыпты координаталардағы екі еркіндік дәрежесі бар жүйенің еріксіз тербеліс теңдеулері бір-бірінен тәуелсіз және бөлек интегралдауға болады.

Мазалаушы күштің критикалық жиіліктері

Теңдеуі қалыпты координаталар өзгерісінің тербелмелі сипатын анықтайды немесе түзу сызық бойындағы нүктенің мәжбүрлі тербелісін қарастыру кезінде егжей-тегжейлі зерттеледі, өйткені қозғалыстың дифференциалдық теңдеулері екі жағдайда да бірдей. Атап айтқанда, егер мазалаушы күштің жиілігі жүйенің табиғи тербелістерінің бірінің жиілігіне тең болса немесе онда шешім фактор ретінде t уақытын қосады. Демек, жеткілікті үлкен t үшін қалыпты жалпыланған координаттардың бірі ерікті түрде үлкен болады немесе бізде резонанс құбылысы болады.