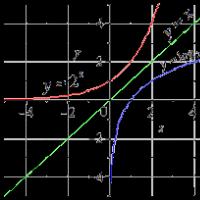
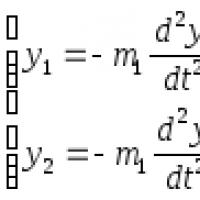Берілген у 2х кері функциясы. Функциялардың түрлері. Кері функция. Функцияның анықталу облысы және мәннің облысы. Кері функцияны табу

Берілген f функциясын және оның аргументінің берілген мәнін ескере отырып, осы нүктеде функцияның мәнін есептеу қажет болатын мәселеге біз бұрыннан тап болдық. Бірақ кейде кері есеппен бетпе-бет келуге тура келеді: белгілі f функциясы берілген және оның белгілі y мәні берілген функция у мәнін алатын аргументтің мәнін табу.

Өзінің әрбір мәнін анықтау облысындағы бір нүктеде алатын функция инвертивті функция деп аталады. Мысалы, сызықтық функция болады инвертивті функция. Бірақ квадраттық функция немесе синус функциясы инверсияланбайтын функциялар болмайды. Өйткені функция әртүрлі аргументтермен бірдей мәнді қабылдай алады.

Кері функция

f қандай да бір ерікті инвертивті функция деп есептейік. Өзінің y0 мәндерінің облысындағы әрбір сан x0 анықтау облысындағы бір ғана санға сәйкес келеді, осылайша f(x0) = y0.

Енді әрбір x0 мәнін y0 мәнімен байланыстырсақ, біз жаңа функция аламыз. Мысалы, f(x) = k * x + b сызықтық функциясы үшін g(x) = (x - b)/k функциясы оған кері болады.

Егер қандай да бір функция gәр нүктеде X f инверсиялық функциясының мәндер диапазоны f(y) = x болатын мәнді қабылдайды, онда функция деп айтамыз g- f функциясына кері функция бар.

Егер бізге қандай да бір инверсияланбайтын f функциясының графигі берілсе, онда кері функцияның графигін тұрғызу үшін келесі мәлімдемені қолдануға болады: f функциясының графигі және оның кері функциясы g түзуге қатысты симметриялы болады. y = x теңдеуі арқылы анықталған сызық.

Егер g функциясы f функциясына кері функция болса, онда g функциясы инвертивті функция болады. Ал f функциясы g функциясына кері функция болады. Әдетте f және g екі функциясы бір-біріне кері болады деп айтылады.

Келесі суретте өзара кері f және g функцияларының графиктері көрсетілген.

Келесі теореманы шығарайық: егер f функциясы қандай да бір А интервалында өссе (немесе кемитін болса), онда ол инверсивті болады. f функциясының мәндер диапазонында анықталған кері функция g, сонымен қатар өсетін (немесе сәйкесінше кеметін) функция болып табылады. Бұл теорема деп аталады кері функция теоремасы.

Бізде x ∈ a анықтау облысында қатаң монотонды (кемімелі немесе өсетін) және үздіксіз болатын белгілі y = f (x) функциясы бар деп есептейік; b ; оның мәндер диапазоны y ∈ c ; d, және с интервалында; d бұл жағдайда мәндер диапазоны x = g (y) анықталған функцияға ие боламыз a ; б. Екінші функция да үздіксіз және қатаң монотонды болады. y = f (x) мәніне қатысты ол кері функция болады. Яғни, y = f (x) берілген аралықта не азаяды, не өсетін кезде кері x = g (y) функциясы туралы айтуға болады.

Бұл екі функция, f және g, өзара кері болады.

Неліктен бізге кері функциялар тұжырымдамасы қажет?

Бұл бізге осы өрнектердің көмегімен дәл жазылған у = f (x) теңдеулерін шешу үшін қажет.

cos (x) = 1 3 теңдеуінің шешімін табу керек делік. Оның шешімдері барлық нүктелер болады: x = ± a rc c o s 1 3 + 2 π · k, k ∈ Z

Мысалы, кері косинус пен косинус функциялары бір-біріне кері болады.

Берілгендерге кері функцияларды табу үшін бірнеше есептерді қарастырайық.

1-мысал

Шарты: y = 3 x + 2 үшін кері функция қандай?

Шешім

Шартта көрсетілген функцияның анықтамалар облысы мен мәндер диапазоны барлық нақты сандар жиыны болып табылады. Бұл теңдеуді х арқылы, яғни х-ті у арқылы өрнектеу арқылы шешуге тырысайық.

Біз x = 1 3 y - 2 3 аламыз. Бұл бізге керегі кері функция, бірақ мұнда у аргумент, ал х функция болады. Таныс белгілерді алу үшін оларды қайта реттейік:

Жауап: y = 1 3 x - 2 3 функциясы у = 3 x + 2-ге кері функция болады.

Өзара кері функциялардың екеуін де төмендегідей графикке салуға болады:

Біз екі графиктің де симметриясын y = x-ке қатысты көреміз. Бұл түзу бірінші және үшінші квадранттардың биссектрисасы болып табылады. Біз өзара кері функциялардың бір қасиетінің дәлелін алдық, оны кейінірек қарастырамыз.

Берілген көрсеткіштік функцияға кері функция болатын логарифмдік функцияны табу керек болатын мысалды алайық.

2-мысал

Шарты: y = 2 x үшін қай функция кері функция болатынын анықтаңыз.

Шешім

Берілген функция үшін анықтау облысы барлық нақты сандар болып табылады. Мәндер диапазоны 0 интервалында жатыр; + ∞ . Енді х-ті у арқылы өрнектеу керек, яғни көрсетілген теңдеуді х арқылы шешу керек. Біз x = log 2 y аламыз. Айнымалыларды қайта реттеп, у = log 2 x алайық.

Нәтижесінде біз анықтаудың барлық аймағында бір-біріне өзара кері болатын көрсеткіштік және логарифмдік функцияларды алдық.

Жауап: y = log 2 x .

Графикте екі функция да келесідей болады:

Өзара кері функциялардың негізгі қасиеттері

Бұл абзацта y = f (x) және x = g (y) функцияларының негізгі қасиеттерін келтіреміз, олар өзара кері.

Анықтама 1

1. Біз бірінші сипатты бұрын шығардық: y = f (g (y)) және x = g (f (x)).
2. Екінші қасиет біріншіден туындайды: y = f (x) анықтау облысы кері x = g (y) функциясының мәндер ауқымымен сәйкес келеді және керісінше.
3. Кері функциялардың графиктері у = х-ке қатысты симметриялы болады.
4. Егер y = f (x) өссе, онда x = g (y) өседі, ал егер y = f (x) кемісе, x = g (y) да кемиді.

Функциялардың анықтау облысы мен мағына облысы ұғымдарына мұқият назар аударуға және оларды ешқашан шатастырмауға кеңес береміз. Бізде y = f (x) = a x және x = g (y) = log a y өзара кері екі функциясы бар деп алайық. Бірінші қасиет бойынша y = f (g (y)) = a log a y. Бұл теңдік у оң мәндері болған жағдайда ғана дұрыс болады, ал теріс мәндер үшін логарифм анықталмаған, сондықтан лог a y = y деп жазуға асықпаңыз. Тек у оң болғанда ғана дұрыс екенін тексеріңіз және қосыңыз.

Бірақ x = f (g (x)) = log a a x = x теңдігі x-тің кез келген нақты мәндері үшін дұрыс болады.

Бұл тармақты ұмытпаңыз, әсіресе тригонометриялық және кері тригонометриялық функциялармен жұмыс істеу керек болса. Сонымен, a r c sin sin 7 π 3 ≠ 7 π 3, өйткені арксинус диапазоны π 2; π 2 және 7 π 3 оған кірмейді. Дұрыс жазба болады

a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = a r c sin sin π 3 = π 3

Бірақ sin a r c sin 1 3 = 1 3 дұрыс теңдік, яғни. sin (a r c sin x) = x үшін x ∈ - 1 ; 1 және a r c sin (sin x) = x үшін x ∈ - π 2 ; π 2. Әрқашан кері функциялардың ауқымы мен ауқымына абай болыңыз!

• Негізгі өзара кері функциялар: қуат функциялары

Егер бізде у = x a дәреже функциясы болса, онда x > 0 үшін х = у 1 а дәреже функциясы да оған кері болады. Әріптерді ауыстырып, сәйкесінше y = x a және x = y 1 a мәнін алайық.

Графикте олар келесідей болады (а оң және теріс коэффициенті бар жағдайлар):

• Негізгі өзара кері функциялар: көрсеткіштік және логарифмдік

А алайық, ол 1-ге тең емес оң сан болады.

a > 1 және a болатын функцияларға арналған графиктер< 1 будут выглядеть так:

• Негізгі өзара кері функциялар: тригонометриялық және кері тригонометриялық

Егер біз синус пен доғаның негізгі тармағын салғымыз келсе, ол келесідей болады (ерекшеленген жарық аймағы ретінде көрсетіледі).

Сабақтың мақсаттары:

Тәрбиелік:

• бағдарламалық материалға сәйкес жаңа тақырып бойынша білімдерін дамыту;
• функцияның қайтымдылық қасиетін зерттеп, берілген функцияның кері функциясын табуды үйрету;

Дамытушылық:

• өзін-өзі бақылау дағдыларын, мазмұнды сөйлеуді дамыту;
• кері функция ұғымын меңгеру және кері функцияны табу әдістерін меңгеру;

Тәрбиелік: коммуникативтік құзыреттіліктерін дамыту.

Жабдық:компьютер, проектор, экран, интерактивті тақта SMART тақта, топтық жұмысқа үлестірмелі материалдар (өздік жұмыс).

Сабақтар кезінде.

1. Ұйымдастыру кезеңі.

Мақсат – Оқушыларды сабақтағы жұмысқа дайындау:

Қатыспағандардың анықтамасы,

Оқушылардың жұмысқа деген көңіл-күйін арттыру, зейінін ұйымдастыру;

Сабақтың тақырыбы мен мақсатын айту.

2. Оқушылардың негізгі білімдерін жаңарту.Фронтальды шолу.

Мақсат - оқытылатын теориялық материалдың дұрыстығы мен хабардарлығын орнату, өтілген материалды қайталау.<Приложение 1 >

Оқушыларға интерактивті тақтада функцияның графигі көрсетілген. Мұғалім тапсырманы тұжырымдайды – функцияның графигін қарастырады және функцияның зерттелген қасиеттерін тізеді. Оқушылар зерттеу жобасына сәйкес функцияның қасиеттерін тізімдейді. Мұғалім функция графигінің оң жағында интерактивті тақтаға маркер арқылы аталған қасиеттерді жазады.

Функция қасиеттері:

Сабақ соңында мұғалім бүгін сабақта функцияның тағы бір қасиеті – қайтымдылығымен танысатындарын хабарлайды. Жаңа материалды мазмұнды оқу үшін мұғалім балаларды сабақтың соңында оқушылар жауап беруі керек негізгі сұрақтармен танысуға шақырады. Сұрақтар кәдімгі тақтаға жазылады және әр оқушыға үлестірмелі материал болады (сабақ алдында таратылады)

1. Қай функция инвертивті деп аталады?
2. Кез келген функция инверсияланбайды ма?
3. Қандай функция деректерге кері функция деп аталады?
4. Функцияның анықтау облысы мен мәндер жиыны және оның кері байланысы қандай?
5. Егер функция аналитикалық түрде берілсе, кері функцияны формула арқылы қалай анықтауға болады?
6. Егер функция графикалық түрде берілсе, оның кері функциясының графигін қалай салуға болады?

3. Жаңа материалды түсіндіру.

Мақсат - бағдарламалық материалға сәйкес жаңа тақырып бойынша білім қалыптастыру; функцияның қайтымдылық қасиетін зерттеу және берілген функцияның кері функциясын табуды үйрету; мазмұнды сөйлеуді дамыту.

Мұғалім абзацтағы материалға сәйкес материалды ұсынады. Интерактивті тақтада мұғалім анықтау облыстары мен мәндер жиыны бірдей, бірақ функцияларының бірі монотонды, екіншісі монотонды емес екі функцияның графиктерін салыстырады, осылайша оқушыларды инверсиялық функция ұғымымен таныстырады. .

Содан кейін мұғалім инверсиялық функцияның анықтамасын тұжырымдап, интерактивті тақтадағы монотонды функцияның графигін пайдаланып инверсиялық функция теоремасын дәлелдейді.

1-анықтама: y=f(x), x X функциясы шақырылады қайтымды, егер ол өзінің мәндерінің кез келгенін Х жиынының бір нүктесінде ғана қабылдаса.

Теорема: Егер y=f(x) функциясы Х жиынында монотонды болса, онда ол инверсиялы болады.

Дәлелдеу:

1. Функция болсын y=f(x)артады Xоны жібер x 1 ≠x 2- жиынның екі нүктесі X.
2. Нақтырақ айтсақ, рұқсат етіңіз x 1< x 2.
   Содан кейін бұл фактіден x 1< x 2соны ұстанады f(x 1) < f(x 2).
3. Осылайша, аргументтің әртүрлі мәндері функцияның әртүрлі мәндеріне сәйкес келеді, яғни. функциясы инвертивті.

(Теореманы дәлелдеу барысында мұғалім сызба бойынша барлық қажетті түсіндірмелерді жасау үшін маркерді пайдаланады)

Кері функцияның анықтамасын тұжырымдамас бұрын мұғалім оқушыларға ұсынылған функциялардың қайсысы инверсиялы екенін анықтауды сұрайды? Интерактивті тақта функциялардың графиктерін көрсетеді және бірнеше аналитикалық анықталған функцияларды жазады:

B)

G) y = 2x + 5

D) y = -x 2 + 7

Мұғалім кері функцияның анықтамасымен таныстырады.

Анықтама 2: Инвертивті функция болсын y=f(x)жиынтықта анықталады XЖәне E(f)=Y. Әрқайсысын сәйкестендірейік жбастап Ыжалғыз мағынасы осы X, онда f(x)=y.Содан кейін біз анықталған функцияны аламыз Ы, А X– функция ауқымы

Бұл функция тағайындалған x=f -1 (y)және функцияға кері функция деп аталады y=f(x).

Студенттерге анықтау облысы мен кері функциялардың мәндер жиыны арасындағы байланыс туралы қорытынды жасау ұсынылады.

Берілген функцияның кері мәнін қалай табуға болады деген сұрақты қарастыру үшін мұғалім екі оқушыны тартты. Балалар бір күн бұрын мұғалімнен берілген функцияның кері функциясын табудың аналитикалық және графикалық әдістерін өз бетінше талдауға тапсырма алды. Мұғалім оқушыларды сабаққа дайындауда кеңесші қызметін атқарды.

Бірінші оқушының хабарламасы.

Ескерту: функцияның монотондылығы болып табылады жеткіліктікері функцияның болу шарты. Бірақ бұл емесқажетті шарт.

Студент функцияның монотонды емес, инверсиялы, функция монотонды емес және инвертивті емес болғанда, монотонды және инверсиялы болатын әртүрлі жағдайларға мысалдар келтірді.

Содан кейін студент студенттерді аналитикалық жолмен берілген кері функцияны табу әдісімен таныстырады.

Алгоритмді табу

1. Функцияның монотонды екеніне көз жеткізіңіз.
2. х айнымалысын у арқылы өрнектеңіз.
3. Айнымалылардың атын өзгерту. x=f -1 (y) орнына y=f -1 (x) деп жазыңыз.

Содан кейін берілгенге кері функцияны табу үшін екі мысалды шешеді.

1-мысал: y=5x-3 функциясы үшін кері функция бар екенін көрсетіңіз және оның аналитикалық өрнегін табыңыз.

Шешім. y=5x-3 сызықтық функциясы R-де анықталған, R-де артады және оның мәндер диапазоны R. Бұл кері функцияның R-де бар екенін білдіреді. Оның аналитикалық өрнегін табу үшін y=5x- теңдеуін шешіңіз. x үшін 3; Бұл қажетті кері функцияны аламыз. Ол R бойынша анықталады және өседі.

2-мысал: y=x 2, x≤0 функциясы үшін кері функция бар екенін көрсетіңіз және оның аналитикалық өрнегін табыңыз.

Функция үзіліссіз, анықтау облысы бойынша монотонды, сондықтан ол инвертивті. Функцияның анықтау облыстары мен мәндер жиынын талдай отырып, кері функцияның аналитикалық өрнек туралы сәйкес қорытынды жасалады.

Екінші оқушы презентация жасайды графикакері функцияны табу әдісі. Түсіндіру барысында оқушы интерактивті тақтаның мүмкіндіктерін пайдаланады.

y=f(x) функциясына кері y=f -1 (x) функциясының графигін алу үшін y=f(x) функциясының графигін түзу сызыққа қатысты симметриялы түрлендіру қажет. y=x.

Интерактивті тақтада түсіндіру барысында келесі тапсырма орындалады:

Бір координаталар жүйесінде функцияның графигін және оның кері функциясының графигін тұрғыз. Кері функцияның аналитикалық өрнегін жазыңыз.

4. Жаңа материалды алғашқы бекіту.

Мақсат - оқытылатын материалды түсінудің дұрыстығы мен хабардарлығын орнату, материалды алғашқы түсінудегі олқылықтарды анықтау және оларды түзету.

Оқушылар жұпқа бөлінеді. Оларға тапсырмалар парақтары беріледі, оларда жұппен жұмыс жасайды. Жұмысты аяқтау уақыты шектеулі (5-7 минут). Бір жұп оқушы компьютерде жұмыс істейді, осы уақыт ішінде проектор өшеді, ал қалған балалар оқушылардың компьютерде қалай жұмыс істейтінін көре алмайды.

Уақыт аяқталғаннан кейін (оқушылардың көпшілігі жұмысты орындады деп есептелінеді) интерактивті тақтада оқушылардың жұмысы көрсетіледі (проектор қайта қосылады), онда тапсырма орындалғаны немесе орындалмағаны тексеру барысында анықталады. жұпта дұрыс орындалды. Қажет болған жағдайда мұғалім түзету және түсіндіру жұмыстарын жүргізеді.

Жұптық жұмыс<2-қосымша >

5. Сабақты қорытындылау.Дәріс алдында қойылған сұрақтарға қатысты. Сабақ бойынша бағаларды хабарлау.

Үйге тапсырма §10. № 10.6(а,в) 10.8-10.9(б) 10.12(б)

Алгебра және талдаудың бастаулары. 10-сынып Жалпы білім беру мекемелеріне арналған 2 бөлікте (бейіндік деңгей) / А.Г.Мордкович, Л.О.Корешкова, т.б.; өңдеген А.Г.Мордкович, М: Мнемосине, 2007 ж

Кері функцияның анықтамасы және оның қасиеттері: тура және кері функциялардың өзара монотондылығы туралы лемма; тура және кері функциялардың графиктерінің симметриясын; кесіндіде, интервалда және жартылай интервалда қатаң монотонды болатын функция үшін кері функцияның бар болуы және үздіксіздігі туралы теоремалар. Кері функциялардың мысалдары. Мәселені шешудің мысалы. Қасиеттер мен теоремаларды дәлелдеу.

Мазмұны

Сондай-ақ қараңыз: Функцияның анықтамасы, жоғарғы және төменгі шекаралары, монотонды функция.

Анықтамасы және қасиеттері

Кері функцияның анықтамасы
Функцияның анықталу облысы X және Y мәндерінің жиыны болсын. Оның меншігіне ие болсын:
барлығына .
Сонда Y жиынының кез келген элементі үшін Х жиынының бір ғана элементін байланыстыруға болады, ол үшін . Бұл сәйкестік деп аталатын функцияны анықтайды кері функция-ге.
.

Кері функция келесі түрде белгіленеді:
;
Анықтамадан былай шығады
барлығына .

барлығына ;
Тура және кері функциялардың графиктерінің симметрия қасиеті

Тура және кері функциялардың графиктері түзуге қатысты симметриялы.
Интервалдағы кері функцияның бар болуы және үзіліссіздігі туралы теорема

Функция үзіліссіз және кесіндіде қатаң өсетін (кемімелі) болсын. Сонда кері функция анықталған және үзіліссіз кесіндіде, ол қатаң түрде артады (кемітеді).

Көбею функциясы үшін. Азайту үшін - .
Интервалдағы кері функцияның бар болуы және үзіліссіздігі туралы теорема

Функция үздіксіз және ашық ақырлы немесе шексіз интервалда қатаң өсетін (кемімелі) болсын. Сонда кері функция анықталған және үзіліссіз интервалда, ол қатаң түрде артады (кемітеді).
Көбею функциясы үшін.

Азайту үшін: .

Сол сияқты біз жарты интервалдағы кері функцияның бар болуы мен үзіліссіздігі туралы теореманы тұжырымдай аламыз.

Егер функция үзіліссіз болса және жарты интервалда қатаң өсетін (кемітетін) болса немесе , онда жартылай интервалда немесе кері функция анықталады, ол қатаң түрде артады (кемітеді). Мұнда .
Егер қатаң өсетін болса, онда интервалдар және интервалдарға сәйкес келеді және . Егер қатаң түрде кемитін болса, онда интервалдар және интервалдарға сәйкес және .

Кері функциялардың мысалдары

арксинус

y = графиктері күнә xжәне кері функциясы y = arcsin x.

Тригонометриялық функцияны қарастырайық синус: . Ол аргументтің барлық мәндері үшін анықталған және үздіксіз, бірақ монотонды емес. Дегенмен, анықтау ауқымын тарылтсаңыз, монотонды аймақтарды анықтауға болады. Сонымен, сегментте функция анықталған, үздіксіз, қатаң түрде өседі және мәндерді алады -1 бұрын +1 . Сондықтан оның арксинус деп аталатын кері функциясы бар. Арксинустың анықтау облысы мен мәндер жиыны бар.

Логарифм

y = графиктері 2 xжәне кері функциясы y = журнал 2 x.

Көрсеткіштік функция анықталған, үздіксіз және аргументтің барлық мәндері үшін қатаң өсетін. Оның мән жиыны ашық интервал болып табылады. Кері функция екі негіздің логарифмі болып табылады. Оның анықтау аймағы мен мағыналар жиынтығы бар.

Шаршы түбір

y = x графиктері 2 және кері функция.

Қуат функциясы барлығы үшін анықталған және үздіксіз. Оның мәндерінің жиыны жарты интервал болып табылады. Бірақ бұл аргументтің барлық мәндері үшін монотонды емес. Дегенмен, жарты интервалда ол үздіксіз және қатаң монотонды түрде артады. Сондықтан анықтау облысы ретінде жиынды алсақ, онда квадрат түбір деп аталатын кері функция бар. Кері функцияның анықталу облысы және мәндер жиыны болады.

Мысал. n дәрежелі түбірдің бар және бірегейлігін дәлелдеу

n – натурал сан, нақты теріс емес сан болатын теңдеуінің нақты сандар жиынында бірегей шешімі бар екенін дәлелдеңдер, . Бұл шешім а-ның n-ші түбірі деп аталады. Яғни, кез келген теріс емес санның n дәрежесінің бірегей түбірі бар екенін көрсету керек.

x айнымалысының функциясын қарастырайық:
(P1) .

Оның үздіксіз екенін дәлелдейміз.
Үздіксіздік анықтамасын пайдалана отырып, біз мұны көрсетеміз
.
Ньютонның биномдық формуласын қолданамыз:
(P2)
.
Функция шектерінің арифметикалық қасиеттерін қолданайық. болғандықтан, тек бірінші мүшесі нөлге тең емес:
.
Үздіксіздігі дәлелденді.

(A1) функциясының ретінде қатаң түрде өсетінін дәлелдейміз.
Теңсіздіктер арқылы қосылған ерікті сандарды алайық:
, , .
Біз мұны көрсетуіміз керек. Айнымалыларды енгізейік. Содан кейін.
.
болғандықтан, содан кейін (А2) дан екені анық. Немесе

Қатаң өсу дәлелденді.
функциясының мәндер жиынын табайық.
нүктесінде,.
Шекті табайық.
.
Ол үшін Бернулли теңсіздігін қолданамыз. Бізде болғанда:
Содан бері, содан кейін және.
Шексіз үлкен функциялар үшін теңсіздіктер қасиетін қолданып, мынаны табамыз.

Кері функция теоремасы бойынша кері функция анықталған және интервалда үздіксіз болады. Яғни, кез келген адам үшін теңдеуді қанағаттандыратын бірегейі бар. Бізде болғандықтан, бұл кез келген , теңдеудің x санының n дәрежелі түбірі деп аталатын бірегей шешімі бар екенін білдіреді:
.

Қасиеттер мен теоремаларды дәлелдеу

Тура және кері функциялардың өзара монотондылығы туралы лемманы дәлелдеу

Функцияның анықталу облысы X және Y мәндерінің жиыны болсын. Оның кері функциясы бар екенін дәлелдейік. Оған сүйене отырып, біз мұны дәлелдеуіміз керек
барлығына .

Керісінше делік. Сандар болсын, сондықтан . Солай болсын. Әйтпесе, белгіні болатындай етіп өзгертейік. Сонда f-тің қатаң монотондылығына байланысты теңсіздіктердің бірі қанағаттандырылуы керек:
f қатаң өсетін болса;
f қатаң түрде төмендейтін болса.
Яғни . Қарама-қайшылық пайда болды. Сондықтан оның кері функциясы бар.

Функция қатаң түрде өссін. Кері функцияның да қатаң өсетінін дәлелдейік. Келесі белгілерді енгізейік:
. Яғни, егер , онда екенін дәлелдеуіміз керек.

Керісінше делік. Болсын, бірақ.

Егер, онда. Бұл жағдай жоғалады.

рұқсат етіңіз.

Сонда , , немесе функциясының қатаң өсуіне байланысты. Қарама-қайшылық пайда болды. Сондықтан тек мүмкіндік болуы мүмкін.

Лемманың қатаң өсетін функциясы дәлелденген. Бұл лемманы қатаң төмендететін функция үшін дәл осылай дәлелдеуге болады.

Тура және кері функциялардың графиктерінің симметриясының қасиетін дәлелдеу
(2.1) .
Тура функцияның графигіндегі ерікті нүкте болсын:
.
Түзуге қатысты А нүктесіне симметриялы нүкте кері функцияның графигіне жататынын көрсетейік:
(2.2) .
Кері функцияның анықтамасынан мынадай қорытынды шығады

Осылайша, (2.2) көрсетуіміз керек. y = f кері функциясының графигі-1(x) y = f тура функциясының графигіне симметриялы(x)

y = x түзуіне қатысты.
, .

А және S нүктелерінен координаталар осіне перпендикулярлар жүргіземіз. Содан кейін

А нүктесі арқылы түзуге перпендикуляр түзу жүргіземіз. Түзулер С нүктесінде қиылыссын. Түзу сызыққа S нүктесін тұрғызамыз. Сонда S нүктесі түзу сызыққа қатысты А нүктесіне симметриялы болады.
.

Үшбұрыштарды және . Олардың ұзындығы бірдей екі қабырғасы бар: және , және олардың арасындағы тең бұрыштар: . Сондықтан олар сәйкес келеді. Содан кейін
.
Үшбұрышты қарастырайық. Сол уақыттан бері
.
Бұл үшбұрышқа да қатысты:
.

Содан кейін
;
.

Енді біз табамыз және:
(2.2)
Сонымен, (2.2) теңдеу:
(2.1) .

қанағаттандырылады, өйткені , және (2.1) орындалады:
функция графигінің түзу сызыққа қатысты симметриялы түрде бейнеленген барлық нүктелері кері функцияның графигіне жатады.
Әрі қарай біз орындарды ауыстыра аламыз. Нәтижесінде біз мұны аламыз
функция графигінің түзу сызыққа қатысты симметриялы түрде бейнеленген барлық нүктелері функция графигіне жатады.
Бұдан шығатыны және функцияларының графиктері түзу сызыққа қатысты симметриялы.

Меншік дәлелденді.

Интервалдағы кері функцияның бар болуы және үзіліссіздігі туралы теореманы дәлелдеу

Функцияның анықталу облысын – кесіндіні белгілейік.

1. Функция мәндерінің жиыны сегмент екенін көрсетейік:
,
Қайда.

Шынында да, функция кесіндіде үзіліссіз болғандықтан, Вейерштрас теоремасы бойынша ол ондағы минимум мен максимумға жетеді. Содан кейін, Болзано-Коши теоремасы бойынша функция сегменттен барлық мәндерді алады. Яғни, кез келген адам үшін бар, ол үшін. Минимум және максимум болғандықтан, функция сегментке жиыннан тек мәндерді қабылдайды.

2. Функция қатаң монотонды болғандықтан, жоғарыда айтылғанға сәйкес кері функция бар, ол да қатаң монотонды (өссе өседі, азайса азаяды). Кері функцияның анықталу облысы жиын, ал мәндер жиыны жиын болып табылады.

3. Енді кері функцияның үзіліссіз екенін дәлелдейміз.

3.1. Кесіндінің ерікті ішкі нүктесі болсын: . Кері функцияның осы нүктеде үзіліссіз болатынын дәлелдейік.

Нүкте соған сәйкес болсын. Кері функция қатаң монотонды болғандықтан, яғни кесіндінің ішкі нүктесі:
.
Үздіксіздік анықтамасына сәйкес, кез келген үшін мұндай функция бар екенін дәлелдеу керек
(3.1) барлығына .

Назар аударыңыз, біз оны қалағанымызша қабылдай аламыз. Шынында да, егер біз (3.1) теңсіздіктері жеткілікті аз мәндері үшін орындалатын функцияны тапсақ, онда біз -ге қойсақ, -ның кез келген үлкен мәндері үшін олар автоматты түрде орындалады.

Нүктелері сегментке жататындығы соншалықты кішкентай болсын:
.
Белгіні енгізіп, реттейік:



.

Бірінші теңсіздікті (3.1) түрлендірейік:
(3.1) барлығына .
;
;
;
(3.2) .
Ол қатаң монотонды болғандықтан, содан кейін шығады
(3.3.1) , егер ол өссе;
(3.3.2) , егер ол төмендесе.
Кері функция да қатаң монотонды болғандықтан, (3.3) теңсіздіктер (3.2) теңсіздіктерді білдіреді.

Кез келген ε үшін > 0 δ бар, сондықтан |f -1 (у) - f -1 (у 0) |< ε барлығы үшін |y - y 0 | < δ .

Теңсіздіктер (3.3) ұштары және қашықтықтағы нүктеден қашық болатын ашық интервалды анықтайды. Осы қашықтықтардың ең кішісі болсын:
.
, , -ның қатаң монотондылығына байланысты. Сондықтан . Сонда интервал (3.3) теңсіздіктермен анықталған интервалда болады. Ал оған жататын барлық мәндер үшін теңсіздіктер (3.2) қанағаттандырылады.

Сондықтан біз кішкентай үшін бар екенін анықтадық, сондықтан
кезінде.
Енді белгіні өзгертейік.
Кішкентай үшін мұндай нәрсе бар, сондықтан
кезінде.
Бұл кері функцияның ішкі нүктелерде үздіксіз болатынын білдіреді.

3.2. Енді анықтау аймағының ұштарын қарастырыңыз. Бұл жерде барлық дәлелдер өзгеріссіз қалады. Сізге тек осы нүктелердің бір жақты аудандарын ескеру қажет. Нүктенің орнына немесе, ал нүктенің орнына - немесе болады.

Сонымен, өсу функциясы үшін , .
кезінде.
Кері функция нүктеде үзіліссіз болады, өйткені кез келген жеткілікті кіші үшін бар, сондықтан
кезінде.

Азаймалы функция үшін, .
Кері функция нүктеде үзіліссіз болады, өйткені кез келген жеткілікті кіші үшін бар, сондықтан
кезінде.
Кері функция нүктеде үзіліссіз болады, өйткені кез келген жеткілікті кіші үшін бар, сондықтан
кезінде.

Теорема дәлелденді.

Интервалдағы кері функцияның бар болуы және үзіліссіздігі туралы теореманы дәлелдеу

Функцияның анықталу облысын – ашық интервалды белгілейік. Оның мәндерінің жиыны болсын. Жоғарыда айтылғандарға сәйкес, анықтау облысы, мәндер жиыны бар және қатаң монотонды болып табылатын кері функция бар (ол өссе өседі және азайса азаяды). Мұны дәлелдеу бізге қалды
1) жиын ашық интервал, және бұл
2) оған кері функция үздіксіз.
Мұнда .

1. Функция мәндерінің жиыны ашық интервал екенін көрсетейік:
.

Элементтерінде салыстыру әрекеті бар кез келген бос емес жиын сияқты, функция мәндерінің жиынының төменгі және жоғарғы шекаралары болады:
.
Мұнда және соңғы сандар немесе символдар және болуы мүмкін.

1.1. және нүктелері функция мәндерінің жиынына жатпайтынын көрсетейік. Яғни, мәндер жиыны сегмент бола алмайды.

Егер немесе болса шексіздік нүктесі: немесе , онда мұндай нүкте жиынның элементі емес. Сондықтан ол бірнеше мәндерге тиесілі бола алмайды.

(немесе ) шекті сан болсын. Керісінше делік. (немесе ) нүкте функция мәндерінің жиынына жататын болсын. Яғни, бұл үшін (немесе) бар. Ұпайларды алып, теңсіздіктерді қанағаттандырайық:
.
Функция қатаң монотонды болғандықтан, онда
, егер f артады;
, егер f азайса.
Яғни, функцияның мәні кіші (үлкен) болатын нүктені таптық. Бірақ бұл төменгі (жоғарғы) шекараның анықтамасына қайшы келеді, оған сәйкес
барлығына .
Сондықтан нүктелер функция мәндерінің жиынына жатпайды.

1.2. Енді мәндер жиыны интервалдар мен нүктелердің бірігуі емес, интервал екенін көрсетеміз. Яғни, кез келген нүкте үшін бар , ол үшін .

Infimum және supremum анықтамаларына сәйкес нүктелердің кез келген көршілестігі және жиынның кем дегенде бір элементін қамтиды. интервалына жататын ерікті сан болсын: . Содан кейін көршілестік бар, ол үшін
.
Аудан үшін бар, ол үшін
.

Содан бері және, содан кейін. Содан кейін
(4.1.1) өссе;
(4.1.2) төмендесе.
(4.1) теңсіздіктерді қайшылық арқылы дәлелдеу оңай. Бірақ сіз пайдалана аласыз, оған сәйкес жиынтықта кері функция бар, ол жоғарыласа, ол қатаң түрде артады және азайса, қатаң төмендейді. Сонда бірден теңсіздіктерді аламыз (4.1).

Сонымен, бізде егер өсетін сегмент бар;
төмендесе.
Сегменттің соңында функция және мәндерін қабылдайды. Өйткені, Болзано-Коши теоремасына сәйкес, оның нүктесі бар.

Содан бері біз осылайша кез келген адам үшін бар екенін көрсеттік. Бұл функцияның мәндер жиыны ашық интервал екенін білдіреді.

2. Енді кері функцияның интервалдың ерікті нүктесінде үзіліссіз болатынын көрсетеміз: . Мұны істеу үшін сегментке қолданыңыз. Өйткені, кері функция кесіндіде, оның ішінде нүктесінде үздіксіз болады.

Теорема дәлелденді.

Қолданылған әдебиет:
О.И. Бесов. Математикалық талдау бойынша дәрістер. 1-бөлім. Мәскеу, 2004 ж.
СМ. Никольский. Математикалық талдау курсы. 1-том. Мәскеу, 1983 ж.

Сондай-ақ қараңыз:

$X$ және $Y$ жиындары нақты сандар жиынына қосылсын. Инверсияланбайтын функция ұғымын енгізейік.

Анықтама 1

$X$ жиынын $Y$ жиынына салыстыратын $f:X\to Y$ функциясы, $x_1\ne x_2$ мәніне сәйкес X$ ішіндегі $x_1,x_2\ элементтерінің кез келгені үшін инвертивті деп аталады. бұл $f(x_1 )\ne f(x_2)$.

Енді біз кері функция ұғымын енгізе аламыз.

Анықтама 2

$X$ жиынын $Y$ жиынына салыстыратын $f:X\to Y$ функциясы инверсиялы болсын. Содан кейін $f^(-1)\left(y\right)=x$ шартымен анықталған $Y$ жиынын $X$ жиынына салыстыратын $f^(-1):Y\-X$ функциясы болып табылады. $f( x)$ үшін кері деп атады.

Теореманы тұжырымдаймыз:

Теорема 1

$y=f(x)$ функциясы белгілі бір $X$ интервалында монотонды өсетін (кемімелі) және үздіксіз болатын болсын. Сонда осы функция мәндерінің сәйкес $Y$ интервалында ол кері функцияға ие болады, ол да монотонды түрде артады (кемітеді) және $Y$ интервалында үздіксіз болады.

Енді өзара кері функциялар ұғымын тікелей енгізейік.

Анықтама 3

2-анықтама шеңберінде $f(x)$ және $f^(-1)\left(y\right)$ функциялары өзара кері функциялар деп аталады.

Өзара кері функциялардың қасиеттері

$y=f(x)$ және $x=g(y)$ функциялары өзара кері болсын, онда

$y=f(g\сол(y\оң))$ және $x=g(f(x))$

$y=f(x)$ функциясының анықталу облысы $\ x=g(y)$ функциясының мәнінің анықталу облысына тең. Ал $x=g(y)$ функциясының анықталу облысы $\ y=f(x)$ функциясының мән анықталу облысына тең.

$y=f(x)$ және $x=g(y)$ функцияларының графиктері $y=x$ түзуіне қатысты симметриялы.

Функциялардың бірі өссе (кемітсе), екінші функция артады (кемітіледі).

Кері функцияны табу

$y=f(x)$ теңдеуі $x$ айнымалысына қатысты шешіледі.

Алынған түбірлерден $X$ интервалына жататындар табылады.

Табылған $x$ $y$ санына сәйкес келеді.

1-мысал

$X=[-1,0]$ интервалында $y=x^2$ функциясына кері функцияны табыңыз.

Бұл функция $X$ интервалында кемитін және үздіксіз болғандықтан, $Y=$ интервалында, ол да осы интервалда кемитін және үздіксіз болады (1-теорема).

$x$ есептейік:

\ \

Сәйкес $x$ таңдаңыз:

Жауап:кері функция $y=-\sqrt(x)$.

Кері функцияларды табуға есептер

Бұл бөлімде кейбір қарапайым функциялар үшін кері функцияларды қарастырамыз. Біз жоғарыда келтірілген схема бойынша мәселелерді шешеміз.

2-мысал

$y=x+4$ функциясына кері функцияны табыңыз

$y=x+4$ теңдеуінен $x$ табайық:

3-мысал

$y=x^3$ функциясына кері функцияны табыңыз

Шешім.

Функция анықтаудың барлық облысы бойынша өсетін және үздіксіз болғандықтан, 1-теоремаға сәйкес, оның кері үздіксіз және өсетін функциясы бар.

$y=x^3$ теңдеуінен $x$ табайық:

$x$ сәйкес мәндерін табу

Мән біздің жағдайда қолайлы (анықтау облысы барлық сандар болғандықтан)

Айнымалыларды қайта анықтайық, кері функцияның пішіні бар екенін аламыз

4-мысал

$$ интервалында $y=cosx$ функциясына кері функцияны табыңыз

Шешім.

$X=\left$ жиынындағы $y=cosx$ функциясын қарастырайық. Ол $X$ жиынында үздіксіз және кемиді және $X=\left$ жиынын $Y=[-1,1]$ жиынына салыстырады, сондықтан кері үздіксіз монотонды функцияның бар екендігі туралы теорема бойынша, $y=cosx$ функциясы $ Y$ жиынында кері функция бар, ол да $Y=[-1,1]$ жиынында үздіксіз және өсетін және $[-1,1]$ жиынын картаға түсіреді. $\left$ жиынына.

$y=cosx$ теңдеуінен $x$ табайық:

$x$ сәйкес мәндерін табу

Айнымалыларды қайта анықтайық, кері функцияның пішіні бар екенін аламыз

5-мысал

$\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ интервалында $y=tgx$ функциясына кері функцияны табыңыз.

Шешім.

$X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ жиынындағы $y=tgx$ функциясын қарастырайық. Ол $X$ жиынында үздіксіз және өседі және $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ жиынын $Y жиынына салыстырады. =R$, демек, кері үздіксіз монотонды функцияның бар екендігі туралы теорема бойынша $Y$ жиынындағы $y=tgx$ функциясы кері функцияға ие, ол да $Y=R жиынында үздіксіз және өсетін болады. $ және $R$ жиынын $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$ жиынымен салыстырады.

$y=tgx$ теңдеуінен $x$ табайық:

$x$ сәйкес мәндерін табу

Айнымалыларды қайта анықтайық, кері функцияның пішіні бар екенін аламыз