Kinukuha ang logarithm. Ano ang isang Logarithm? Solusyon ng logarithms. Mga halimbawa. Mga pag-aari ng logarithms. Mga halimbawa ng paglutas ng mga logarithm batay sa mga formula

Logarithm ng numero N sa pamamagitan ng katwiran at tinawag na exponent x kung saan nais mong itayo at upang makuha ang numero N

Ibinigay iyon
,
,

Sumusunod ito mula sa kahulugan ng isang logarithm na
, ibig sabihin
- ang pagkakapantay-pantay na ito ay ang pangunahing pagkakakilanlan ng logarithmic.

Ang Logarithms base 10 ay tinatawag na decimal logarithms. Sa halip
sumulat
.

Mag-base ang Logarithms e tinatawag na natural at denoted
.

Pangunahing katangian ng logarithms.

Ang Logarithm ng isa para sa anumang base ay zero

Ang logarithm ng produkto ay katumbas ng kabuuan ng mga logarithm ng mga salik.

3) Ang logarithm ng quotient ay katumbas ng pagkakaiba ng mga logarithms

Salik
tinatawag na modulus ng paglipat mula sa logarithms sa base a sa logarithms sa base b .

Sa tulong ng mga pag-aari 2-5, madalas na posible na bawasan ang logarithm ng isang kumplikadong expression sa resulta ng simpleng pagpapatakbo ng arithmetic sa mga logarithm.

Halimbawa,

Ang mga nasabing pagbabago ng logarithm ay tinatawag na logarithms. Ang mga pagbabago na kabaligtaran sa logarithm ay tinatawag na potentiation.

Kabanata 2. Mga elemento ng mas mataas na matematika.

1. Mga limitasyon

Limitasyon ng pagpapaandar
ay isang may hangganan na numero A kung, bilang xx 0 para sa bawat preset
, mayroong isang bilang
na minsan
tapos
.

Ang isang pagpapaandar na may isang limitasyon ay naiiba mula dito sa pamamagitan ng isang walang katapusang maliit na halaga:
, nasaan ang isang b.m.v., ibig sabihin
.

Halimbawa. Isaalang-alang ang pagpapaandar
.

Kapag nagsusumikap
, pagpapaandar y ay may gawi sa zero:

1.1. Pangunahing mga teorya sa mga limitasyon.

Ang limitasyon ng isang pare-pareho na halaga ay katumbas ng pare-parehong halagang ito

.

Ang hangganan ng kabuuan (pagkakaiba) ng isang may hangganan na bilang ng mga pag-andar ay katumbas ng kabuuan (pagkakaiba) ng mga limitasyon ng mga pagpapaandar na ito.

Ang limitasyon ng produkto ng isang may hangganan na bilang ng mga pagpapaandar ay katumbas ng produkto ng mga limitasyon ng mga pagpapaandar na ito.

Ang limitasyong limitasyon ng dalawang pag-andar ay katumbas ng kabuuan ng mga limitasyon ng mga pagpapaandar na ito kung ang limitasyon ng denominator ay hindi zero.

Kamangha-manghang mga limitasyon

,
kung saan

1.2. Limitahan ang Mga Halimbawa ng Pagkalkula

Gayunpaman, hindi lahat ng mga limitasyon ay madaling kalkulahin. Mas madalas, ang pagkalkula ng limitasyon ay nabawasan sa pagsisiwalat ng isang kawalan ng katiyakan tulad ng: o.

.

2. Hango ng pagpapaandar

Magkaroon tayo ng isang pagpapaandar
tuloy-tuloy sa segment
.

Argumento nakakuha ng dagdag
... Pagkatapos ang function ay makakatanggap ng isang pagtaas
.

Halaga ng argumento tumutugma sa halaga ng pag-andar
.

Halaga ng argumento
tumutugma sa halaga ng pag-andar.

Dahil dito,.

Hahanapin natin ang hangganan ng ratio na ito sa
... Kung umiiral ang limitasyong ito, kung gayon ito ay tinatawag na hango ng pagpapaandar na ito.

Kahulugan 3 Hango ng pagpapaandar na ito
sa pamamagitan ng pagtatalo ay tinawag na hangganan ng ratio ng pagtaas ng pagpapaandar sa pagtaas ng argumento, kung ang pagtaas ng argumento ay arbitraryong may gawi na zero.

Pag-andar ng hango
maaaring italaga tulad ng sumusunod:

; ; ; .

Kahulugan 4 Ang pagpapatakbo ng paghahanap ng hango ng isang pagpapaandar ay tinawag pagkita ng pagkakaiba-iba.

2.1. Ang mekanikal na kahulugan ng hinalaw.

Isaalang-alang ang paggalaw ng rectilinear ng ilang matibay na katawan o materyal na punto.

Hayaan sa ilang mga punto ng oras gumagalaw na punto
nasa malayo mula sa panimulang posisyon
.

Maya-maya
lumayo siya ng malayo
... Saloobin =- average na bilis ng isang materyal na punto
... Hahanapin natin ang hangganan ng ratio na ito, isinasaalang-alang iyon
.

Dahil dito, ang pagtukoy ng instant na bilis ng isang materyal na punto ay nabawasan sa paghahanap ng hinalaw ng landas sa oras.

2.2. Hango sa halagang geometriko

Hayaan mo kaming magkaroon ng isang grapikong ibinigay ng ilang pagpapaandar
.

Larawan: 1. Heometriko kahulugan ng hinalang

Kung
pagkatapos ay ituro
, lilipat sa kurba, papalapit sa punto
.

Dahil dito
, ibig sabihin ang halaga ng hinalang binigyan ng halaga ng argumento ayon sa bilang na katumbas ng tangent ng anggulo na nabuo ng tangent sa isang naibigay na punto na may positibong direksyon ng axis
.

2.3. Talaan ng pangunahing mga formula para sa pagkita ng pagkakaiba.

Pag-andar ng kuryente

Exponential function

Pag-andar ng Logarithmic

Trigonometric function

Baliktad na pag-andar ng trigonometric

2.4. Mga panuntunan sa pagkakaiba-iba.

Hango sa

Hango ng kabuuan (pagkakaiba) ng mga pagpapaandar

Hango ng produkto ng dalawang pag-andar

Hango ng kabuuan ng dalawang pag-andar

2.5. Hango sa kumplikadong pag-andar.

Hayaan ang pagpapaandar
tulad na maaari itong kumatawan bilang

at
kung saan variable ay isang intermediate na argument, kung gayon

Ang hango ng isang kumplikadong pag-andar ay katumbas ng produkto ng hango ng pagpapaandar na ito patungkol sa intermedyang argumento ng hango ng intermedyang argumento na may paggalang sa x.

Halimbawa 1.

Halimbawa 2.

3. Pagkakaiba ng pagpapaandar.

Hayaan na
naiiba sa ilang segment
pakawalan sa ang paggana na ito ay may isang hango

,

pagkatapos ay maaari kaming magsulat

(1),

kung saan - walang katapusang maliit na halaga,

mula pa noong

Pagpaparami ng lahat ng mga tuntunin ng pagkakapantay-pantay (1) ng
meron kami:

Kung saan
- b.m.v. mas mataas na kaayusan.

Ang dami
ay tinatawag na kaugalian ng pagpapaandar
at tinukoy

.

3.1. Ang halagang geometriko ng kaugalian.

Hayaan ang pagpapaandar
.

Larawan 2. Ang kahulugan ng geometriko ng pagkakaiba.

.

Malinaw na ang pagkakaiba ng pagpapaandar
ay katumbas ng pagtaas ng ordinate ng tangent sa puntong ito.

3.2. Mga derivatives at kaugalian ng iba't ibang mga order.

Kung meron
tapos
tinawag na unang hango.

Ang hango ng unang hango ay tinatawag na pangalawang-hango na hango at nakasulat
.

Hango ng ika-n na pagkakasunud-sunod ng pagpapaandar
ang hango ng (n-1) -th order ay tinawag at nakasulat:

.

Ang kaugalian ng kaugalian ng isang pag-andar ay tinatawag na pangalawang kaugalian o ang pangalawang kaugalian sa pagkakasunud-sunod.

.

.

3.3 Paglutas ng mga problemang biyolohikal gamit ang pagkita ng pagkakaiba-iba.

Gawain 1. Ipinakita ng mga pag-aaral na ang paglago ng isang kolonya ng mga mikroorganismo ay sumusunod sa batas
kung saan N - ang bilang ng mga mikroorganismo (sa libo-libo), t –Panahon (araw).

b) Ang laki ba ng kolonya ay tataas o babaan sa panahong ito?

Sagot Ang kolonya ay lalago sa laki.

Gawain 2. Ang tubig sa lawa ay pana-panahong sinusubukan upang makontrol ang nilalaman ng mga pathogenic bacteria. Sa kabila t araw pagkatapos ng pagsubok, ang konsentrasyon ng bakterya ay natutukoy ng ratio

.

Kailan darating ang minimum na konsentrasyon ng bakterya sa lawa at posible itong lumangoy dito?

SOLUSYON Ang isang pagpapaandar ay umabot sa max o min kapag ang derivative nito ay zero.

,

Tukuyin natin ang max o min ay nasa 6 na araw. Para sa mga ito kinukuha namin ang pangalawang derivative.

Sagot: Pagkatapos ng 6 na araw, magkakaroon ng minimum na konsentrasyon ng bakterya.

Tulad ng alam mo, kapag nagpaparami ng mga expression sa mga kapangyarihan, ang kanilang mga exponent ay laging nagdaragdag (a b * a c \u003d a b + c). Ang batas sa matematika na ito ay nagmula sa Archimedes, at kalaunan, noong ika-8 siglo, lumikha ang matematiko na si Virasen ng isang talahanayan ng buong mga tagapagpahiwatig. Sila ang nagsilbi para sa karagdagang pagtuklas ng logarithms. Ang mga halimbawa ng paggamit ng pagpapaandar na ito ay matatagpuan halos saanman kung saan mo nais gawing simple ang isang masalimuot na pagdami sa pamamagitan ng simpleng pagdaragdag. Kung gugugol ka ng 10 minuto sa pagbabasa ng artikulong ito, ipapaliwanag namin sa iyo kung ano ang mga logarithms at kung paano gumana sa kanila. Sa simple at naa-access na wika.

Kahulugan sa matematika

Ang logarithm ay isang ekspresyon ng sumusunod na form: log ab \u003d c, iyon ay, ang logarithm ng anumang di-negatibong numero (iyon ay, anumang positibo) na "b" batay sa batayan nito na "a" ay ang kapangyarihan na "c", kung saan ang batayang "a" ay dapat itaas, upang magwakas kunin ang halagang "b". Pag-aralan natin ang logarithm gamit ang mga halimbawa, halimbawa, mayroong isang expression log 2 8. Paano mahahanap ang sagot? Napakadali, kailangan mong maghanap ng gayong degree na mula sa 2 hanggang sa nais na degree na nakukuha mo sa 8. Natapos na ang ilang mga kalkulasyon sa iyong isip, nakukuha namin ang numero 3! At tama, dahil ang 2 sa lakas ng 3 ay nagbibigay ng bilang 8 sa sagot.

Mga pagkakaiba-iba ng logarithms

Para sa maraming mga mag-aaral at mag-aaral, ang paksang ito ay tila kumplikado at hindi maintindihan, ngunit sa katunayan, ang mga logarithm ay hindi gaanong nakakatakot, ang pangunahing bagay ay upang maunawaan ang kanilang pangkalahatang kahulugan at alalahanin ang kanilang mga pag-aari at ilang mga patakaran. Mayroong tatlong magkakaibang uri ng ekspresyon ng logarithmic:

1. Likas na logarithm ln a, kung saan ang base ay ang bilang ni Euler (e \u003d 2.7).
2. Desimal a, batayan 10.
3. Logarithm ng anumang bilang b upang ibase ang isang\u003e 1.

Ang bawat isa sa kanila ay nalulutas sa isang pamantayan na paraan, kasama ang pagpapasimple, pagbawas at kasunod na pagbawas sa isang logarithm gamit ang logorithmic theorems. Upang makuha ang mga tamang halaga ng logarithms, dapat mong tandaan ang kanilang mga pag-aari at ang pagkakasunud-sunod ng mga aksyon kapag nilulutas ito.

Mga panuntunan at ilang mga paghihigpit

Sa matematika, maraming mga patakaran-paghihigpit na tinatanggap bilang isang axiom, iyon ay, hindi sila maaaring makipag-ayos at totoo. Halimbawa, hindi mo maaaring hatiin ang mga numero sa zero, at imposible ring kumuha ng pantay na ugat ng mga negatibong numero. Ang mga Logarithms ay mayroon ding sariling mga panuntunan, na sinusundan kung saan madali mong matutunan na gumana kahit na may mahaba at magaling na ekspresyon ng logarithmic:

• ang batayang "a" ay dapat palaging mas malaki kaysa sa zero, at sa parehong oras ay hindi katumbas ng 1, kung hindi man mawawala ang kahulugan nito, dahil ang "1" at "0" sa anumang degree ay palaging katumbas ng kanilang mga halaga;
• kung ang isang\u003e 0, pagkatapos ay isang b\u003e 0, lumalabas na ang "c" ay dapat ding mas malaki sa zero.

Paano malutas ang mga logarithm?

Halimbawa, binigyan ang gawain ng paghahanap ng sagot sa equation 10 x \u003d 100. Napakadali, kailangan mong pumili ng ganoong degree, taasan ang bilang na sampu na nakukuha natin sa 100. Ito, syempre, 10 2 \u003d 100.

Kinakatawan natin ngayon ang expression na ito bilang isang logarithmic. Nakukuha namin ang log 10 100 \u003d 2. Kapag nalulutas ang mga logarithms, lahat ng mga aksyon ay halos nagtatagpo upang makahanap ng lakas kung saan kinakailangan upang ipakilala ang base ng logarithm upang makuha ang ibinigay na numero.

Upang tumpak na matukoy ang halaga ng isang hindi kilalang degree, kinakailangan upang malaman kung paano gumana sa talahanayan ng mga degree. Parang ganito:

Tulad ng nakikita mo, ang ilang mga exponents ay maaaring nahulaan nang intuitively kung mayroon kang isang teknikal na pag-iisip at kaalaman sa talahanayan ng pagpaparami. Gayunpaman, mangangailangan ang isang mas malaking halaga ng isang talahanayan ng kuryente. Maaari itong magamit kahit ng mga hindi nakakaintindi ng anuman tungkol sa mga kumplikadong paksa sa matematika. Ang kaliwang haligi ay naglalaman ng mga numero (base a), ang nangungunang hilera ng mga numero ay ang lakas c kung saan ang numero a ay itinaas. Sa intersection sa mga cell, ang mga halaga ng mga numero ay tinukoy, na kung saan ay ang sagot (a c \u003d b). Kunin natin, halimbawa, ang pinakaunang cell na may bilang na 10 at parisukat ito, nakukuha natin ang halagang 100, na ipinahiwatig sa interseksyon ng aming dalawang mga cell. Napakadali at madali ang lahat na kahit na ang pinaka totoong humanista ay mauunawaan!

Mga katumbas at hindi pagkakapantay-pantay

Ito ay lumiliko na sa ilalim ng ilang mga kundisyon ang exponent ay ang logarithm. Samakatuwid, ang anumang pagpapahayag na may bilang na matematika ay maaaring nakasulat bilang isang pagkakapantay-pantay ng logarithmic. Halimbawa, ang 3 4 \u003d 81 ay maaaring maisulat bilang logarithm ng 81 hanggang sa base 3, katumbas ng apat (log 3 81 \u003d 4). Para sa mga negatibong kapangyarihan, ang mga patakaran ay pareho: 2 -5 \u003d 1/32, isinusulat namin ito bilang isang logarithm, nakakuha kami ng log 2 (1/32) \u003d -5. Ang isa sa mga nakakaakit na lugar ng matematika ay ang paksang "logarithms". Isasaalang-alang namin ang mga halimbawa at solusyon ng mga equation nang kaunti sa ibaba, kaagad pagkatapos pag-aralan ang kanilang mga pag-aari. Ngayon tingnan natin kung ano ang hitsura ng mga hindi pagkakapantay-pantay at kung paano makilala ang mga ito mula sa mga equation.

Ang isang pagpapahayag ng sumusunod na form ay ibinigay: mag-log 2 (x-1)\u003e 3 - ito ay hindi pagkakapareho ng logarithmic, dahil ang hindi kilalang halaga na "x" ay nasa ilalim ng pag-sign ng logarithm. At gayun din sa ekspresyon, dalawang halaga ang inihambing: ang logarithm ng kinakailangang numero sa base dalawa ay mas malaki kaysa sa bilang tatlo.

Ang pinakamahalagang pagkakaiba sa pagitan ng mga katumbas na logarithmic at hindi pagkakapantay-pantay ay ang mga equation na may logarithms (halimbawa, logarithm 2 x \u003d √9) ay nagpapahiwatig ng isa o higit pang mga tukoy na mga numerong halaga sa sagot, habang ang paglutas ng hindi pagkakapantay-pantay ay tumutukoy sa parehong saklaw ng mga tinatanggap na halaga at mga puntos sinisira ang pagpapaandar na ito. Bilang kinahinatnan, ang sagot ay hindi isang simpleng hanay ng magkakahiwalay na mga numero tulad ng sa sagot sa equation, ngunit isang tuluy-tuloy na serye o hanay ng mga numero.

Pangunahing mga teorya sa logarithms

Kapag nalulutas ang mga sinaunang gawain upang hanapin ang mga halaga ng logarithm, maaaring hindi alam ang mga pag-aari nito. Gayunpaman, pagdating sa logarithmic equation o hindi pagkakapantay-pantay, una sa lahat, kinakailangan upang malinaw na maunawaan at mailapat sa pagsasanay ang lahat ng pangunahing mga katangian ng logarithms. Malalaman natin ang mga halimbawa ng mga equation mamaya, pag-aralan muna natin ang bawat pag-aari nang mas detalyado.

1. Ang pangunahing pagkakakilanlan ay ganito ang hitsura: isang logaB \u003d B. Nalalapat lamang ito kung ang a ay mas malaki sa 0, hindi katumbas ng isa, at ang B ay mas malaki sa zero.
2. Ang logarithm ng produkto ay maaaring kinatawan sa sumusunod na pormula: log d (s 1 * s 2) \u003d log d s 1 + log d s 2. Sa kasong ito, ang isang paunang kinakailangan ay: d, s 1 at s 2\u003e 0; isang ≠ 1. Maaari kang magbigay ng isang patunay para sa pormulang ito ng logarithms, na may mga halimbawa at solusyon. Hayaang mag-log bilang 1 \u003d f 1 at mag-log bilang 2 \u003d f 2, pagkatapos ay isang f1 \u003d s 1, isang f2 \u003d s 2. Nakukuha namin iyon s 1 * s 2 \u003d a f1 * a f2 \u003d a f1 + f2 (mga pag-aari ng mga kapangyarihan ), at higit pa, sa pamamagitan ng kahulugan: mag-log a (s 1 * s 2) \u003d f 1 + f 2 \u003d mag-log ng s1 + log bilang 2, na kinakailangan upang mapatunayan.
3. Ang logarithm ng quient ay ganito: mag-log a (s 1 / s 2) \u003d mag-log a s 1 - mag-log ng s 2.
4. Ang teorama sa anyo ng isang pormula ay kumukuha ng sumusunod na form: mag-log a q b n \u003d n / q mag-log a b.

Ang formula na ito ay tinatawag na "pag-aari ng degree ng logarithm". Ito ay kahawig ng mga katangian ng mga ordinaryong degree, at hindi nakakagulat, dahil ang lahat ng matematika ay nakasalalay sa natural na postulate. Tingnan natin ang katibayan.

Hayaang mag-log a b \u003d t, lumalabas na isang t \u003d b. Kung taasan natin ang parehong bahagi sa lakas m: a tn \u003d b n;

ngunit dahil sa isang tn \u003d (a q) nt / q \u003d b n, samakatuwid mag-log ng q b n \u003d (n * t) / t, pagkatapos ay mag-log ng q b n \u003d n / q log a b. Pinatunayan ang teorya.

Mga halimbawa ng mga problema at hindi pagkakapantay-pantay

Ang pinaka-karaniwang uri ng mga problema sa logarithm ay mga halimbawa ng mga equation at inequalities. Matatagpuan ang mga ito sa halos lahat ng mga librong may problema, at kasama rin sa sapilitan na bahagi ng mga pagsusulit sa matematika. Para sa pagpasok o paghahatid sa unibersidad pagsusulit sa pasukan sa matematika, kailangan mong malaman kung paano malulutas nang tama ang mga nasabing gawain.

Sa kasamaang palad, walang iisang plano o pamamaraan para sa paglutas at pagtukoy ng hindi kilalang halaga ng logarithm, gayunpaman, ang ilang mga patakaran ay maaaring mailapat sa bawat hindi pagkakapantay-pantay sa matematika o equation ng logarithmic. Una sa lahat, kinakailangan upang malaman kung ang pagpapahayag ay maaaring gawing simple o dalhin sa isang pangkalahatang form. Maaari mong gawing simple ang mahabang mga expression ng logarithmic kung gagamitin mo nang tama ang kanilang mga pag-aari. Kilalanin natin sila agad.

Kapag nalulutas ang mga equation ng logarithmic, kinakailangan upang matukoy kung anong uri ng logarithm ang nasa harap natin: isang halimbawa ng isang expression ay maaaring maglaman ng isang natural na logarithm o decimal.

Narito ang mga halimbawa ln100, ln1026. Ang kanilang solusyon ay umuusbong sa katotohanan na kailangan mong matukoy ang antas kung saan ang batayan 10 ay katumbas ng 100 at 1026, ayon sa pagkakabanggit. Para sa mga solusyon ng natural na logarithms, kailangan mong maglapat ng mga pagkakakilanlang logarithmic o kanilang mga pag-aari. Tingnan natin ang mga halimbawa ng paglutas ng mga problema sa logarithmic ng iba't ibang uri.

Paano gumamit ng mga formula ng logarithm: may mga halimbawa at solusyon

Kaya, tingnan natin ang mga halimbawa ng paggamit ng pangunahing mga teorya sa logarithms.

1. Ang pag-aari ng logarithm ng produkto ay maaaring magamit sa mga gawain kung saan kinakailangan upang mabulok ang isang malaking halaga ng bilang b sa mas simpleng mga kadahilanan. Halimbawa, mag-log 2 4 + log 2 128 \u003d mag-log 2 (4 * 128) \u003d mag-log 2 512. Ang sagot ay 9.
2. log 4 8 \u003d log 2 2 2 3 \u003d 3/2 log 2 2 \u003d 1.5 - tulad ng nakikita mo, na inilalapat ang ika-apat na pag-aari ng lakas ng logarithm, posible na malutas ang isang tila kumplikado at hindi malulutas na ekspresyon. Kailangan mo lamang i-factor ang base sa mga kadahilanan at pagkatapos ay kunin ang mga halaga ng kuryente mula sa pag-sign ng logarithm.

Mga gawain mula sa pagsusulit

Ang Logarithms ay madalas na matatagpuan sa mga pagsusulit sa pasukan, lalo na ang maraming mga problema sa logarithmic sa pagsusulit (pagsusulit sa estado para sa lahat ng nagtapos sa paaralan). Karaniwan, ang mga gawaing ito ay naroroon hindi lamang sa bahagi A (ang pinakamadali bahagi ng pagsubok pagsusulit), ngunit din sa bahagi C (ang pinakamahirap at malalaking gawain). Ang pagsusulit ay nagpapahiwatig ng tumpak at perpektong kaalaman ang paksang "Likas na mga logarithm".

Ang mga halimbawa at solusyon sa mga problema ay kinuha mula sa opisyal mga pagpipilian para sa pagsusulit... Tingnan natin kung paano malulutas ang mga nasabing gawain.

Naibigay na log 2 (2x-1) \u003d 4. Solusyon:
muling isulat ang expression, pinapasimple ito ng kaunting log 2 (2x-1) \u003d 2 2, sa pamamagitan ng kahulugan ng logarithm, nakukuha natin ang 2x-1 \u003d 2 4, samakatuwid 2x \u003d 17; x \u003d 8.5.

• Mahusay na i-convert ang lahat ng mga logarithm sa isang base upang ang solusyon ay hindi masalimuot at nakalilito.
• Ang lahat ng mga expression sa ilalim ng pag-sign ng logarithm ay ipinahiwatig bilang positibo, samakatuwid, kapag ang exponent ng exponent ay nakuha ng factor, na nasa ilalim ng pag-sign ng logarithm at bilang batayan nito, ang ekspresyon na natitira sa ilalim ng logarithm ay dapat na positibo.

Habang umuunlad ang lipunan at naging mas kumplikado ang produksyon, umunlad din ang matematika. Ang paglipat mula sa simple patungo sa kumplikado. Mula sa karaniwang accounting sa pamamagitan ng pamamaraan ng pagdaragdag at pagbabawas, sa kanilang paulit-ulit na pag-uulit, napunta kami sa konsepto ng pagpaparami at paghahati. Ang pagbawas ng paulit-ulit na pagpapatakbo ng pagpaparami ay naging konsepto ng exponentiation. Ang mga unang talahanayan ng pag-asa ng mga numero sa base at ang bilang ng pagtaas sa isang kapangyarihan ay naipon noong ika-8 siglo ng dalub-agbilang sa India na si Varasen. Mula sa kanila, maaari mong bilangin ang oras ng paglitaw ng mga logarithms.

Makasaysayang sketch

Ang muling pagkabuhay ng Europa noong ika-16 na siglo ay nagpasigla din sa pag-unlad ng mekanika. T kinakailangan ng isang malaking halaga ng pagkalkulana nauugnay sa pagpaparami at paghahati ng mga numero ng multidigit. Isang mahusay na serbisyo ang mga sinaunang mesa. Ginawa nilang posible na palitan ang mga kumplikadong operasyon ng mas simple - karagdagan at pagbabawas. Ang isang malaking hakbang na pasulong ay ang gawa ng dalubbilang si Michael Stiefel, na inilathala noong 1544, kung saan napagtanto niya ang ideya ng maraming mga dalub-agbilang matematika. Ginawa nitong posible na gumamit ng mga talahanayan hindi lamang para sa mga degree sa anyo ng mga prima, kundi pati na rin para sa di-makatwirang mga makatuwiran.

Noong 1614, ang Scotsman na si John Napier, na bumubuo ng mga ideyang ito, ay unang ipinakilala ang bagong katagang "logarithm ng isang numero". Ang mga bagong kumplikadong talahanayan ay naipon upang makalkula ang logarithms ng sines at cosines, pati na rin ang mga tangents. Lubhang binawasan nito ang gawain ng mga astronomo.

Nagsimulang lumitaw ang mga bagong talahanayan na matagumpay na ginamit ng mga siyentista sa loob ng tatlong siglo. Ito ay tumagal ng isang mahabang oras bago ang isang bagong operasyon sa algebra nakuha ang natapos na form. Ang kahulugan ng logarithm ay ibinigay at ang mga katangian nito ay pinag-aralan.

Noong ika-20 siglo lamang, sa pagkakaroon ng calculator at computer, inabandona ng sangkatauhan ang mga sinaunang mesa na matagumpay na nagtatrabaho sa buong ika-13 siglo.

Tinawag namin ngayon ang logarithm ng b base a bilang bilang x, na kung saan ay isang kapangyarihan ng a, upang gawin ang bilang na b. Ito ay nakasulat sa anyo ng isang pormula: x \u003d log a (b).

Halimbawa, mag-log 3 (9) ay magiging 2. Ito ay halata kung susundin mo ang kahulugan. Kung ang 3 ay itataas sa lakas ng 2, makakakuha tayo ng 9.

Kaya, ang formulated na kahulugan ay nagtatakda lamang ng isang paghihigpit, ang mga numero a at b ay dapat na tunay.

Mga pagkakaiba-iba ng logarithms

Ang klasikal na kahulugan ay tinawag na totoong logarithm at talagang isang solusyon sa equation na a x \u003d b. Ang pagpipiliang a \u003d 1 ay borderline at walang interes. Tandaan: Ang 1 ay katumbas ng 1 sa anumang degree.

Tunay na halaga ng logarithm natukoy lamang kapag ang radix at argument ay mas malaki sa 0, at ang radix ay hindi dapat katumbas ng 1.

Isang espesyal na lugar sa matematika maglaro ng logarithms, na papangalanan depende sa laki ng kanilang base:

Mga panuntunan at paghihigpit

Ang pangunahing pag-aari ng logarithms ay ang panuntunan: ang logarithm ng produkto ay katumbas ng logarithmic sum. mag-log abp \u003d mag-log a (b) + mag-log a (p).

Bilang isang pagkakaiba-iba ng pahayag na ito ay magiging: log c (b / p) \u003d log c (b) - log c (p), ang quotient function ay katumbas ng pagkakaiba ng mga pagpapaandar.

Mula sa nakaraang dalawang mga panuntunan madali itong makita: mag-log a (b p) \u003d p * mag-log a (b).

Ang iba pang mga pag-aari ay kinabibilangan ng:

Magkomento. Huwag gumawa ng isang karaniwang pagkakamali - ang logarithm ng kabuuan ay hindi katumbas ng kabuuan ng mga logarithm.

Sa loob ng maraming daang siglo, ang pagpapatakbo ng paghahanap ng logarithm ay isang masipag na gawain. Ginamit ng mga matematiko ang kilalang pormula ng logarithmic polynomial expansion theory:

ln (1 + x) \u003d x - (x ^ 2) / 2 + (x ^ 3) / 3 - (x ^ 4) / 4 +… + ((-1) ^ (n + 1)) * (( x ^ n) / n), kung saan n - natural na numero mas malaki sa 1, na tumutukoy sa kawastuhan ng pagkalkula.

Ang Logarithms na may iba pang mga base ay kinakalkula gamit ang teorema sa paglipat mula sa isang base patungo sa isa pa at ang pag-aari ng logarithm ng produkto.

Dahil ang pamamaraang ito ay napaka oras at kapag nalulutas ang mga praktikal na problema mahirap ipatupad, pagkatapos ay gumamit kami ng paunang naipon na mga talahanayan ng logarithms, na lubhang pinabilis ang buong gawain.

Sa ilang mga kaso, ginamit ang espesyal na pinagsama-sama na mga graph ng logarithms, na nagbigay ng mas kaunting kawastuhan, ngunit makabuluhang pinabilis ang paghahanap para sa nais na halaga. Ang kurba ng pagpapaandar y \u003d mag-log a (x), na naka-plot sa maraming mga puntos, pinapayagan ang paggamit ng isang regular na pinuno upang hanapin ang mga halaga ng pagpapaandar sa anumang iba pang mga punto. Sa loob ng mahabang panahon, ginamit ng mga inhinyero ang tinatawag na graph paper para sa mga hangaring ito.

Noong ika-17 siglo, lumitaw ang unang kundisyon ng auxiliary analog computational na kung saan noong ika-19 na siglo ay nakuha ang isang kumpletong form. Ang pinakamatagumpay na aparato ay tinatawag na slide panuntunan. Sa lahat ng pagiging simple ng aparato, ang hitsura nito ay makabuluhang pinabilis ang proseso ng lahat ng mga kalkulasyon sa engineering, at mahirap i-overestimate ito. Sa kasalukuyan, ilang tao na ang pamilyar sa aparatong ito.

Ang pagkakaroon ng mga calculator at computer na ginawa itong walang kabuluhan upang gumamit ng anumang iba pang mga aparato.

Mga katumbas at hindi pagkakapantay-pantay

Ang mga sumusunod na formula ay inilalapat upang malutas ang iba't ibang mga equation at inequalities gamit ang logarithms:

• Ang paglipat mula sa isang base patungo sa isa pa: mag-log a (b) \u003d log c (b) / log c (a);
• Bilang kinahinatnan ng nakaraang bersyon: mag-log a (b) \u003d 1 / log b (a).

Upang malutas ang mga hindi pagkakapantay-pantay, kapaki-pakinabang na malaman:

• Ang halaga ng logarithm ay magiging positibo lamang kung ang base at argument ay parehong mas malaki o mas mababa sa isa; kung hindi bababa sa isang kundisyon ay nilabag, ang halaga ng logarithm ay magiging negatibo.
• Kung ang pagpapaandar ng logarithm ay inilalapat sa kanan at kaliwang panig ng isang hindi pagkakapantay-pantay, at ang base ng logarithm ay mas malaki sa isa, kung gayon ang tanda ng hindi pagkakapantay-pantay ay napanatili; kung hindi man, nagbabago ito.

Mga halimbawa ng gawain

Isaalang-alang natin ang maraming mga pagpipilian para sa paggamit ng logarithms at kanilang mga pag-aari. Mga halimbawa sa paglutas ng mga equation:

Isaalang-alang ang pagpipilian ng paglalagay ng logarithm sa kapangyarihan:

• Suliranin 3. Kalkulahin ang 25 ^ log 5 (3). Solusyon: sa ilalim ng mga kundisyon ng problema, ang talaan ay katulad ng sumusunod (5 ^ 2) ^ log5 (3) o 5 ^ (2 * log 5 (3)). Isulat natin ito sa ibang paraan: 5 ^ log 5 (3 * 2), o ang parisukat ng isang numero bilang isang argument sa isang pagpapaandar ay maaaring nakasulat bilang parisukat ng pagpapaandar mismo (5 ^ log 5 (3)) ^ 2. Gamit ang mga katangian ng logarithms, ang ekspresyong ito ay 3 ^ 2. Sagot: bilang isang resulta ng pagkalkula, nakakakuha kami ng 9.

Praktikal na paggamit

Ang pagiging isang pulos tool sa matematika, tila malayo sa totoong buhay na biglang nakuha ng logarithm ang malaking kahalagahan para sa paglalarawan ng mga bagay sa totoong mundo. Mahirap maghanap ng agham kung saan hindi ito inilalapat. Ganap na nalalapat ito hindi lamang sa natural, kundi pati na rin ng mga pantaong pantao ng kaalaman.

Mga dependency sa Logarithmic

Narito ang ilang mga halimbawa ng mga dependency sa bilang:

Mekanika at Physics

Kasaysayan, ang mga mekanika at pisika ay palaging binuo gamit ang mga pamamaraan ng pagsasaliksik sa matematika at sa parehong oras ay nagsilbing isang insentibo para sa pagpapaunlad ng matematika, kabilang ang mga logarithm. Ang teorya ng karamihan sa mga batas ng pisika ay nakasulat sa wika ng matematika. Narito lamang ang dalawang halimbawa ng paglalarawan ng mga pisikal na batas gamit ang logarithm.

Posibleng malutas ang problema sa pagkalkula ng isang kumplikadong dami tulad ng bilis ng isang rocket gamit ang formula ng Tsiolkovsky, na naglagay ng pundasyon para sa teorya ng paggalugad sa kalawakan:

V \u003d I * ln (M1 / M2), kung saan

• Ang V ay ang pangwakas na bilis ng sasakyang panghimpapawid.
• Ako ang tiyak na salpok ng engine.
• Ang M 1 ay ang paunang masa ng rocket.
• Ang M 2 ang pangwakas na misa.

Isa pang mahalagang halimbawa - ito ang ginagamit sa pormula ng isa pang mahusay na siyentista na si Max Planck, na nagsisilbi upang masuri ang estado ng balanse sa mga termodinamika.

S \u003d k * ln (Ω), kung saan

• S - pagmamay-ari ng thermodynamic.
• k ay pare-pareho ang Boltzmann.
• Ang weight ay ang bigat ng istatistika ng iba't ibang mga estado.

Kimika

Ang hindi gaanong halata ay ang paggamit ng mga pormula sa kimika na naglalaman ng ratio ng logarithms. Magbibigay din kami ng dalawang halimbawa:

• Ang equation ni Nernst, ang kalagayan ng potensyal na pagbabawas ng oksihenasyon ng daluyan na may kaugnayan sa aktibidad ng mga sangkap at pare-pareho ang balanse.
• Ang pagkalkula ng mga naturang pare-pareho ng autoprolysis index at ang kaasiman ng solusyon ay hindi rin kumpleto nang wala ang aming pagpapaandar.

Sikolohiya at biology

At ganap na hindi malinaw kung ano ang gagawin sa sikolohiya dito. Ito ay lumalabas na ang lakas ng pandamdam ay mahusay na inilarawan ng pagpapaandar na ito bilang ang kabaligtaran na ratio ng halaga ng kasidhian ng pampasigla sa mas mababang halaga ng kasidhian.

Matapos ang mga halimbawa sa itaas, hindi na nakakagulat na ang paksa ng logarithms ay malawakang ginagamit sa biology. Maaaring isulat ang mga volume tungkol sa mga biological form na naaayon sa logarithmic spirals.

Ibang lugar

Tila imposible ang pagkakaroon ng mundo nang walang koneksyon sa pagpapaandar na ito, at pinamumunuan nito ang lahat ng mga batas. Lalo na kapag ang mga batas ng kalikasan ay naiugnay sa isang pag-unlad na geometriko. Ito ay nagkakahalaga ng pagtukoy sa website ng MatProfi, at maraming mga tulad halimbawa sa mga sumusunod na lugar ng aktibidad:

Ang listahan ay maaaring maging walang hanggan. Ang pagkakaroon ng mastered ang pangunahing mga batas ng pagpapaandar na ito, maaari kang plunge sa mundo ng walang katapusang karunungan.

(mula sa Greek λόγος - "salitang", "ugnayan" at ἀριθμός - "numero") na mga numero b sa pamamagitan ng katwiran a (mag-log α b) ay tinatawag na tulad ng isang numero cat b= isang c, iyon ay, mag-log α b=c at b \u003d a c ay katumbas. Makatuwiran ang logarithm kung ang isang\u003e 0, at ≠ 1, b\u003e 0.

Sa ibang salita logarithm numero b sa pamamagitan ng katwiran atay formulated bilang isang tagapagpahiwatig ng degree na kung saan ang numero ay dapat na itataas aupang makuha ang numero b(ang mga positibong numero lamang ang may isang logarithm).

Ang pagbabalangkas na ito ay nagpapahiwatig na ang computation x \u003d log α b, ay katumbas ng paglutas ng equation a x \u003d b.

Halimbawa:

mag-log 2 8 \u003d 3 dahil 8 \u003d 2 3.

Binibigyang diin namin na ang ipinahiwatig na pagbubuo ng logarithm ay ginagawang posible upang agad na matukoy halaga ng logarithm, kapag ang numero sa ilalim ng pag-sign ng logarithm ay ilang degree ng base. At sa katotohanan, ang pagbabalangkas ng logarithm ay ginagawang posible upang mapatunayan na kung b \u003d a c, pagkatapos ang logarithm ng numero b sa pamamagitan ng katwiran a ay pantay mula sa... Malinaw din na ang paksa ng logarithm ay malapit na nauugnay sa paksa antas ng bilang.

Ang pagkalkula ng logarithm ay tinawag sa pamamagitan ng pagkuha ng logarithm... Ang pagkuha ng logarithm ay ang pagpapatakbo ng matematika ng pagkuha ng logarithm. Kapag kumukuha ng logarithm, ang produkto ng mga kadahilanan ay nabago sa kabuuan ng mga term.

Potensyal ay isang pagpapatakbo ng matematika na kabaligtaran sa logarithm. Sa potentiation, ang naibigay na batayan ay nakataas sa lakas ng ekspresyon kung saan ginanap ang potentiation. Sa kasong ito, ang kabuuan ng mga miyembro ay nabago sa produkto ng mga kadahilanan.

Ang mga totoong logarithm na may mga base 2 (binary), e Euler's number e 7 2.718 (natural logarithm) at 10 (decimal) ay madalas na ginagamit.

Sa yugtong ito, ipinapayong isaalang-alang mga sample ng logarithmsmag-log 7 2 , ln √ 5, lg0.0001.

At ang mga entry na lg (-3), log -3 3.2, log -1 -4.3 ay walang katuturan, dahil sa una sa kanila ang isang negatibong numero ay inilalagay sa ilalim ng pag-sign ng logarithm, sa pangalawa - isang negatibong numero sa base, at sa pangatlo - isang negatibong numero sa ilalim ng pag-sign ng logarithm at isa sa base.

Mga kundisyon para sa pagtukoy ng logarithm.

Ito ay nagkakahalaga ng isasaalang-alang nang hiwalay sa mga kundisyon a\u003e 0, isang ≠ 1, b\u003e 0 sa ilalim ng kung saan kahulugan ng logarithm. Isaalang-alang natin kung bakit kinuha ang mga paghihigpit na ito. Isang pagkakapantay-pantay ng form x \u003d log α b , na tinatawag na pangunahing pagkakakilanlan ng logarithmic, na direktang sumusunod mula sa kahulugan ng isang logarithm na ibinigay sa itaas.

Kunin natin ang kundisyon isang ≠ 1... Dahil ang isa ay katumbas ng isa sa anumang degree, ang pagkakapantay-pantay x \u003d log α b maaari lamang magkaroon kapag b \u003d 1ngunit ang mag-log 1 1 ay magiging anumang tunay na numero. Upang maalis ang kalabuan na ito, kumukuha kami isang ≠ 1.

Patunayan natin ang pangangailangan ng kundisyon isang\u003e 0... Kailan a \u003d 0 ayon sa pagbabalangkas ng logarithm, maaari lamang itong magkaroon para sa b \u003d 0... At nang naaayon pagkatapos mag-log 0 0ay maaaring maging anumang hindi tunay na tunay na numero, dahil ang zero sa anumang degree na nonzero ay zero. Upang ibukod ang kalabuan na ito ay ibinibigay ng kundisyon isang ≠ 0... At kailan a<0 tatanggihan namin ang pagtatasa ng mga makatuwiran at hindi makatwiran na halaga ng logarithm, dahil ang isang degree na may isang makatuwiran at hindi makatuwiran na exponent ay tinukoy lamang para sa mga hindi negatibong batayan. Ito ay para sa kadahilanang ito na ang kondisyon ay nakasaad isang\u003e 0.

At ang huling kondisyon b\u003e 0 sumusunod mula sa hindi pagkakapantay-pantay isang\u003e 0dahil x \u003d log α b, at ang halaga ng degree na may positibong base a laging positibo.

Mga tampok ng logarithms.

Logarithms nailalarawan sa pamamagitan ng natatanging mga tampok, na humantong sa kanilang malawakang paggamit upang makabuluhang mapadali ang mga kalkulasyon ng masakit. Sa paglipat "sa mundo ng logarithms," ang pagpaparami ay binago sa isang mas madaling pagdaragdag, paghahati sa pagbabawas, at pagpapalawak at pagkuha ng ugat ay binago, ayon sa pagkakabanggit, sa pagpaparami at paghahati ng exponent.

Pagbubuo ng mga logarithm at isang talahanayan ng kanilang mga halaga (para sa pagpapaandar ng trigonometric) ay unang nai-publish noong 1614 ng Scottish matematikal na si John Napier. Ang mga talahanayan ng Logarithmic, na pinalaki at detalyado ng iba pang mga siyentista, ay malawakang ginamit sa mga kalkulasyong pang-agham at engineering, at nanatiling may kaugnayan hanggang sa magamit ang mga electronic calculator at computer.

Logarithm positibong numeroN sa pamamagitan ng base( b> 0, b1 ) tinawag na exponentx kung saan nais mong itayo b upang makuha N .

Notasyon ng Logarithm:

Ang entry na ito ay katumbas ng mga sumusunod:b x \u003d N .

Mga halimbawa: mag-log 3 81 \u003d 4, mula noong 3 4 \u003d 81;

Mag-log 1/3 27 \u003d – 3, mula noong (1/3) - 3 \u003d 3 3 \u003d 27.

Ang kahulugan sa itaas ng isang logarithm ay maaaring nakasulat bilang isang pagkakakilanlan:

Pangunahing katangian ng logarithms.

1) mag-log b= 1 , kasi b 1 \u003d b.

b

2) mag-log 1 = 0 , kasi b 0 = 1 .

b

3) Ang logarithm ng produkto ay katumbas ng kabuuan ng logarithms ng mga kadahilanan:

mag-log ( ab) \u003d mag-log a+ mag-log b.

4) Ang logarithm ng kabuuan ay katumbas ng pagkakaiba sa pagitan ng mga logarithm ng dividend at ng tagahati:

mag-log ( a/ b) \u003d mag-log a- mag-log b.

5) Ang logarithm ng kapangyarihan ay katumbas ng produkto ng exponent ng logarithm ng base nito:

mag-log ( b k ) = k Mag-log b.

Ang kinahinatnan ng pag-aari na ito ay ang mga sumusunod:logarithm ng ugat ay katumbas ng logarithm ng root number na hinati ng lakas ng ugat:

6) Kung mayroong isang degree sa base ng logarithm, pagkatapos ay ang halaga ang kabaligtaran ng exponent, maaaring madala sa labas ng log signtula:

Ang huling dalawang pag-aari ay maaaring pagsamahin sa isa:

7) Formula ng module ng paglipat (ibig sabihine ... paglipat mula sa isang base logarithm sa ibang base):

Sa isang partikular na kaso, para sa N \u003d a meron kami:

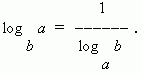
Decimal logarithm tinawag logarithm sa base10. Ito ay itinalaga lg, ibig sabihin mag-log 10 N = lg N ... Logarithms ng mga bilang 10, 100, 1000, ... p avna ayon sa pagkakabanggit 1, 2, 3, ...,mga yan maraming positibo

mga yunit, kung gaano karaming mga zero ang nasa logarithm pagkatapos ng isa. Logarithms ng mga numero 0.1, 0.01, 0.001, ...p avna ayon sa pagkakabanggit –1, –2, –3,…, ibig sabihin ay may maraming mga negatibong tulad ng may mga zero sa logarithm sa harap ng isa ( pagbibilang at zero integers). Logarithms ang natitirang mga numero ay may isang praksyonal na bahagi, na tinatawag na mantissa... Buoang bahagi ng logarithm ay tinawag katangian... Para sa praktikal na paggamitang desimal logarithms ay pinaka-maginhawa.

Likas na logarithm tinawag logarithm sa base e... Ito ay itinalaga ln, ibig sabihin mag-log eN = ln N... Bilang e ay hindi makatuwiran, nitoisang tinatayang halaga ng 2.718281828.Ito ay ang hangganan na kinabibilangan ng bilang(1 + 1 / n) n na may walang limitasyong pagtaas n (cm. unang kahanga-hangang limitasyon ).
Kakatwa na tila, natural na logarithms ay naging napaka-maginhawa para sa pagdala ng iba't ibang mga operasyon na may kaugnayan sa pagtatasa ng mga pag-andar.Kinakalkula ang mga base logarithm enatupad mas mabilis kaysa sa anumang iba pang mga batayan.